Более простая формула для аппроксимации кривой с использованием дуговых сегментов

Таблица ссылок

АННОТАЦИЯ

1 ВВЕДЕНИЕ

2 СГЛАЖИВАНИЕ И АППРОКСИМАЦИЯ КРИВЫХ ДУГАМИ

3 СПИРАЛИ ЭЙЛЕРА И ИХ ПАРАЛЛЕЛЬНЫЕ КРИВЫЕ

4 СГЛАЖЕННЫЕ ПАРАЛЛЕЛЬНЫЕ КРИВЫЕ

5 МЕТРИКИ ОШИБОК ДЛЯ АППРОКСИМАЦИИ ДУГАМИ

6 ЭВОЛЮТЫ

7 ПРЕОБРАЗОВАНИЕ ИЗ КУБИЧЕСКИХ КРИВЫХ БЕЗЬЕ В СПИРАЛИ ЭЙЛЕРА

8 РЕАЛИЗАЦИЯ НА GPU

9 РЕЗУЛЬТАТЫ

ВЫВОДЫ, ДАЛЬНЕЙШАЯ РАБОТА И ССЫЛКИ

\

МЕТРИКИ ОШИБОК ДЛЯ АППРОКСИМАЦИИ ДУГАМИ

Проблема аппроксимации кривой последовательностью дуговых сегментов имеет обширную литературу, но ни одно из опубликованных решений не совсем подходит для нашего приложения. Конкретная проблема аппроксимации спирали Эйлера дугами рассматривается в работе Meek и Walton [2004] с использованием адаптивной схемы подразделения "сначала разрезать, затем измерить", но их решение имеет низкое качество; оно масштабируется как 𝑂(1/𝑛 2 ), в то время как достижимо 𝑂(1/𝑛 3 ). Результат был "немного" улучшен Narayan [2014].

\ Литература также содержит оптимальные результаты, а именно Maier [2014] и Nuntawisuttiwong и Dejdumrong [2021], но со значительными затратами; оба подхода заявляют о временной сложности 𝑂(𝑛 2 ). Общая линия для всех этих результатов заключается в том, что они решают более сложную задачу: принимая ограничение, что сгенерированная последовательность дуг является 𝐺 1 непрерывной. Хотя это желательно для многих приложений, это ограничение не требуется для рендеринга контура штриха.

\ Даже при ослаблении этого ограничения угловые разрывы аппроксимации дугами незначительны по сравнению со сглаживанием до линий. Наш подход основан на простой метрике ошибок, похожей по духу на ту, что используется для сглаживания до линейных сегментов. Детали метрики (в частности, настройка констант) были получены эмпирически, хотя мы подозреваем, что могут быть получены более строгие аналитические границы. На практике это работает действительно очень хорошо; лучший способ наблюдать это - интерактивный инструмент тестирования, который предоставляется в дополнительных материалах.

Предлагаемая метрика ошибок выглядит следующим образом. Оценочная ошибка расстояния для кривой длины 𝑠ˆ составляет:

𝑑 ≈ 1 120 ∫ 𝑠ˆ 0 3 √︁ |𝜅 ′ (𝑠)|𝑑𝑠!3

Для сегмента спирали Эйлера 𝜅 ′ (𝑠) является константой, и, таким образом, эта метрика ошибок становится почти тривиальной. С 𝑛 подразделениями оценочное расстояние просто 𝑠 3𝜅 ′ 120𝑛 3 . Решая для 𝑛, мы получаем 𝑛 = 𝑠 3 √︃ |𝜅 ′ | 120𝑑 подразделений, и они равномерно распределены по длине дуги, так как плотность подразделения постоянна по всей кривой, как и в случае сглаживания дуг до линий. Примечательно, что аппроксимация параллельной кривой спирали Эйлера дуговыми сегментами почти так же проста, как и для спиралей Эйлера к дугам.

\ Как и при сглаживании до линий, параметром для кривой является длина дуги исходной спирали Эйлера. Плотность подразделения затем постоянна, и требуется лишь небольшая корректировка формулы для вычисления количества подразделений, учитывая дополнительное изменение кривизны от смещения на ℎ (половина ширины линии). Пересмотренная формула:

𝑛 = 𝑠 3 √︂ |𝜅 ′ | (1 + 0.4|ℎ𝑠𝜅′ |) 120𝑑

Эта формула была определена эмпирически путем подгонки кривой измеренных значений ошибок от аппроксимации параллельных кривых спирали Эйлера к дугам, но также была вдохновлена применением общей формулы метрики ошибок к аналитическим уравнениям для параллельной кривой спирали Эйлера и отбрасыванием членов высшего порядка. Более строгий вывод, в идеале с твердыми границами ошибок, остается для будущей работы.

\ Одним из следствий этой формулы является то, что, поскольку ошибка выражается в терминах абсолютного значения ℎ, независимо от знака, одна и та же аппроксимация дугой может использоваться для обеих сторон штриха. См. Рисунок 8 для сравнения между сглаживанием до полилинии и аппроксимацией с сегментами дуг. Версия с сегментами дуг имеет гораздо меньше сегментов при той же допустимой погрешности, сохраняя при этом очень высокое визуальное качество.

ЭВОЛЮТЫ

В принципиальной, правильной спецификации для штриховки [19], параллельные кривые достаточны только для сегментов, в которых кривизна

\

\ не превышает обратную полуширину. Когда это происходит, должны быть нарисованы дополнительные сегменты, включая эволюты исходной кривой. В общем случае эволюта кубической кривой Безье является очень сложной кривой, требующей методов аппроксимации. В отличие от этого, эволюта спирали Эйлера (𝜅 = 𝑎𝑠) является другой спиралью с простым уравнением Чезаро, а именно 𝜅 = −𝑎 −1 𝑠 −3 , примером общего результата, что эволюта лог-эстетической кривой является другой лог-эстетической кривой [26].

\ Сглаживание этой эволюты также просто; плотность подразделения пропорциональна 𝑠 −0.5 , где 𝑠 - параметр длины дуги базовой спирали Эйлера (и переведен так, что 𝑠 = 0 является точкой перегиба). Таким образом, интеграл равен 2 √ 𝑠, а обратный интеграл - просто возведение в квадрат. Таким образом, сглаживание эволюты спирали Эйлера проще, чем сглаживание ее параллельной кривой. Э

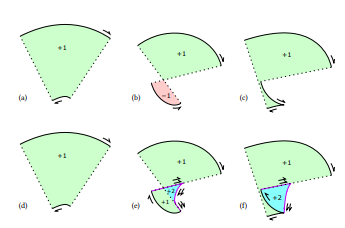
\ ффект добавления эволют для достижения сильной корректности показан на Рисунке 9. Дополнительные сегменты эволют и соединительные линии выводятся дважды, чтобы сделать числа намоток согласованными и создать водонепроницаемый контур. Все числа намоток положительны, поэтому рендеринг с правилом ненулевой намотки дает правильный окончательный рендер.

:::info Авторы:

1. Raph Levien
2. Arman Uguray

:::

:::info Эта статья доступна на arxiv под лицензией CC 4.0.

:::

\