Hiểu về Sai số Xấp xỉ và Độ phức tạp Truy vấn trong Định tuyến WormHole

Bảng liên kết

Tóm tắt và 1. Giới thiệu

1.1 Đóng góp của chúng tôi

1.2 Thiết lập

1.3 Thuật toán

1. Công trình liên quan

2. Thuật toán

   3.1 Giai đoạn phân rã cấu trúc

   3.2 Giai đoạn định tuyến

   3.3 Các biến thể của WormHole

3. Phân tích lý thuyết

   4.1 Kiến thức cơ bản

   4.2 Tính phi tuyến tính của vòng trong

   4.3 Sai số xấp xỉ

   4.4 Độ phức tạp truy vấn

4. Kết quả thực nghiệm

   5.1 WormHole𝐸, WormHole𝐻 và BiBFS

   5.2 So sánh với các phương pháp dựa trên chỉ mục

   5.3 WormHole như một nguyên thủy: WormHole𝑀

Tài liệu tham khảo

4.3 Sai số xấp xỉ

Bây giờ chúng ta đã có một vòng trong phi tuyến tính chứa lõi Chung-Lu, chúng ta phải chứng minh rằng việc định tuyến các đường dẫn thông qua nó chỉ gây ra một mức phạt nhỏ. Theo trực giác, vòng trong càng lớn, việc thỏa mãn điều này càng dễ dàng: nếu vòng trong là toàn bộ đồ thị, phát biểu sẽ đúng một cách hiển nhiên. Do đó, thách thức nằm ở việc chứng minh rằng chúng ta có thể đạt được một đảm bảo mạnh về độ chính xác ngay cả với một vòng trong phi tuyến tính. Chúng tôi chứng minh rằng WormHole gây ra một sai số cộng tối đa là 𝑂(loglog𝑛) cho tất cả các cặp, nhỏ hơn nhiều so với đường kính Θ(log𝑛).

\

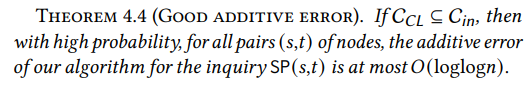
\ Kết quả trên đúng với xác suất cao ngay cả trong trường hợp xấu nhất. Cụ thể, đối với tất cả các cặp (𝑠,𝑡) của các đỉnh trong đồ thị, độ dài của đường dẫn được trả về bởi WormHole cao hơn tối đa 𝑂(loglog𝑛) so với khoảng cách thực tế giữa 𝑠 và 𝑡. Điều này hiển nhiên hàm ý rằng sai số cộng trung bình của WormHole, với xác suất cao, bị giới hạn bởi cùng một lượng.

\

\

4.4 Độ phức tạp truy vấn

Nhắc lại mô hình truy vấn nút trong bài báo này (xem §1.2): bắt đầu từ một nút duy nhất, chúng ta được phép lặp đi lặp lại các truy vấn, trong đó mỗi truy vấn truy xuất danh sách láng giềng của một nút 𝑣 mà chúng ta chọn. Chúng ta quan tâm đến độ phức tạp truy vấn, tức là số lượng truy vấn cần thiết để thực hiện các hoạt động nhất định.

\ \

\ \ Kết quả đầu tiên là giới hạn trên về hiệu suất của chúng ta.

\ \

\ \ Phác thảo chứng minh. Đối với một truy vấn SP(𝑢, 𝑣) đã cho, chúng ta đưa ra một giới hạn trên về độ phức tạp truy vấn của BFS bắt đầu tại 𝑢, và tương tự cho 𝑣; tổng độ phức tạp truy vấn là tổng của hai số lượng này.

\ \

\ \ \

\ \ \

\ \ \

\ \ \

\ \

:::info Tác giả:

(1) Talya Eden, Đại học Bar-Ilan ([e-mail]);

(2) Omri Ben-Eliezer, MIT ([e-mail]);

(3) C. Seshadhri, UC Santa Cruz ([e-mail]).

:::

---

:::info Bài báo này có sẵn trên arxiv theo giấy phép CC BY 4.0.

:::

\