Cách WormHole Tăng Tốc Tìm Đường Trong Đồ Thị Tỷ Cạnh

Bảng liên kết

Tóm tắt và 1. Giới thiệu

1.1 Đóng góp của chúng tôi

1.2 Bối cảnh

1.3 Thuật toán

1. Công trình liên quan

2. Thuật toán

   3.1 Giai đoạn phân tách cấu trúc

   3.2 Giai đoạn định tuyến

   3.3 Các biến thể của WormHole

3. Phân tích lý thuyết

   4.1 Kiến thức cơ bản

   4.2 Tính chất dưới tuyến tính của vòng trong

   4.3 Sai số xấp xỉ

   4.4 Độ phức tạp truy vấn

4. Kết quả thực nghiệm

   5.1 WormHole𝐸, WormHole𝐻 và BiBFS

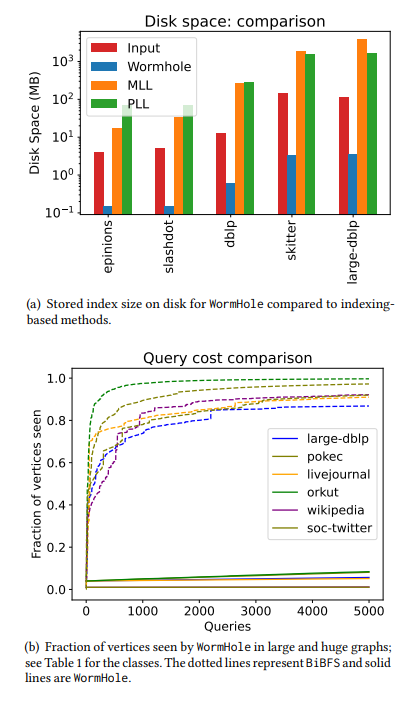
   5.2 So sánh với các phương pháp dựa trên chỉ mục

   5.3 WormHole như một nguyên thủy: WormHole𝑀

Tài liệu tham khảo

1.1 Đóng góp của chúng tôi

Chúng tôi thiết kế một thuật toán mới, WormHole, tạo ra một cấu trúc dữ liệu cho phép chúng tôi trả lời nhiều truy vấn đường đi ngắn nhất bằng cách khai thác cấu trúc điển hình của nhiều mạng xã hội và thông tin. WormHole đơn giản, dễ triển khai và có cơ sở lý thuyết vững chắc. Chúng tôi cung cấp một số biến thể của nó, mỗi biến thể phù hợp với một bối cảnh khác nhau, cho thấy kết quả thực nghiệm xuất sắc trên nhiều bộ dữ liệu mạng khác nhau. Dưới đây là một số tính năng chính:

\ • Đánh đổi giữa hiệu suất và độ chính xác. Theo hiểu biết của chúng tôi, đây là thuật toán đường đi ngắn nhất xấp xỉ dưới tuyến tính đầu tiên trong các mạng lớn. Việc chúng tôi cho phép lỗi cộng thêm nhỏ dẫn đến sự đánh đổi giữa thời gian/không gian tiền xử lý và thời gian cho mỗi truy vấn, và cho phép chúng tôi đưa ra

\

\ một giải pháp với khả năng tiền xử lý hiệu quả và thời gian truy vấn nhanh. Đáng chú ý, biến thể chính xác nhất (nhưng chậm nhất) của chúng tôi, WormHole𝐸, có độ chính xác gần như hoàn hảo: hơn 90% các truy vấn được trả lời mà không có lỗi cộng thêm, và trong tất cả các mạng, hơn 99% các truy vấn được trả lời với lỗi cộng thêm tối đa là 2. Xem Bảng 3 để biết thêm chi tiết.

\ • Thời gian thiết lập cực kỳ nhanh. Thời gian xây dựng chỉ mục lâu nhất của chúng tôi chỉ là hai phút ngay cả đối với các đồ thị có hàng tỷ cạnh. Để hiểu rõ hơn, PLL và MLL đã hết thời gian trên một nửa số mạng mà chúng tôi kiểm tra, và đối với các đồ thị có kích thước vừa phải mà PLL và MLL hoàn thành việc chạy, việc xây dựng chỉ mục WormHole nhanh hơn 100 lần. Cụ thể, WormHole hoàn thành trong vài giây trong khi PLL mất hàng giờ. Xem Bảng 4 và Bảng 5. Thời gian thiết lập nhanh này đạt được nhờ việc sử dụng chỉ mục có kích thước dưới tuyến tính. Đối với các mạng lớn nhất mà chúng tôi xem xét, chỉ cần lấy một chỉ mục khoảng 1% số nút để có lỗi cộng thêm trung bình nhỏ - xem Bảng 1. Đối với các mạng nhỏ hơn, có thể lên đến 6%.

\ • Thời gian truy vấn nhanh. So với BiBFS, phiên bản cơ bản WormHole𝐸 (không có bất kỳ tối ưu hóa dựa trên chỉ mục nào) nhanh hơn 2 lần đối với hầu hết tất cả các đồ thị và nhanh hơn hơn 4 lần trên ba đồ thị lớn nhất mà chúng tôi đã kiểm tra. Một biến thể đơn giản WormHole𝐻 đạt được sự cải thiện về độ lớn với một số chi phí về độ chính xác: nhanh hơn 20 lần trên hầu hết tất cả các đồ thị, và hơn 180 lần đối với đồ thị lớn nhất mà chúng tôi có. Xem Bảng 3 để có so sánh đầy đủ. Các phương pháp dựa trên chỉ mục thường trả lời các truy vấn trong vài micro giây; cả hai biến thể đã đề cập ở trên vẫn ở trong phạm vi mili giây.

\ • Kết hợp WormHole và công nghệ tiên tiến. WormHole hoạt động bằng cách lưu trữ một tập con nhỏ các đỉnh mà chúng tôi tính toán đường đi ngắn nhất chính xác. Đối với các truy vấn tùy ý, chúng tôi định tuyến đường đi của mình thông qua tập con này, mà chúng tôi gọi là lõi. Chúng tôi sử dụng hiểu biết này để cung cấp biến thể thứ ba, WormHole𝑀 bằng cách triển khai công nghệ tiên tiến cho đường đi ngắn nhất, MLL, trên lõi. Điều này đạt được thời gian truy vấn tương đương với MLL (với cùng mức đảm bảo độ chính xác như WormHole𝐻) với chi phí thiết lập chỉ bằng một phần nhỏ, và chạy cho các đồ thị khổng lồ mà MLL không thể hoàn thành. Chúng tôi khám phá phương pháp kết hợp này trong §5.3, và cung cấp số liệu thống kê trong Bảng 6.

\ • Độ phức tạp truy vấn dưới tuyến tính. Độ phức tạp truy vấn đề cập đến số lượng đỉnh được truy vấn bởi thuật toán. Trong một mô hình truy cập truy vấn hạn chế, nơi việc truy vấn một nút tiết lộ danh sách các nút lân cận của nó (xem §1.2), độ phức tạp truy vấn của thuật toán của chúng tôi mở rộng rất tốt với số lượng truy vấn khoảng cách / đường đi ngắn nhất được thực hiện. Để trả lời 5000 truy vấn đường đi ngắn nhất xấp xỉ, thuật toán của chúng tôi chỉ quan sát từ 1% đến 20% số nút đối với hầu hết các mạng. Trong khi đó, BiBFS thấy hơn 90% đồ thị để trả lời vài trăm truy vấn đường đi ngắn nhất. Xem Hình 2 và Hình 5 để so sánh.

\ • Đảm bảo có thể chứng minh về lỗi và hiệu suất. Trong §4, chúng tôi chứng minh một loạt các kết quả lý thuyết bổ sung và giải thích hiệu suất thực nghiệm. Các kết quả, được trình bày không chính thức dưới đây, được chứng minh cho mô hình đồ thị ngẫu nhiên Chung-Lu với phân phối bậc luật lũy thừa [15–17].

\ Định lý 1.1 (Không chính thức). Trong một đồ thị ngẫu nhiên Chung-Lu 𝐺 với số mũ luật lũy thừa 𝛽 ∈ (2,3) trên 𝑛 đỉnh, WormHole có các đảm bảo sau với xác suất cao:

\

\

:::info Tác giả:

(1) Talya Eden, Đại học Bar-Ilan ([e-mail]);

(2) Omri Ben-Eliezer, MIT ([e-mail]);

(3) C. Seshadhri, UC Santa Cruz ([e-mail]).

:::

---

:::info Bài báo này có sẵn trên arxiv theo giấy phép CC BY 4.0.

:::

\