Công thức đơn giản hơn cho phép xấp xỉ đường cong bằng các đoạn cung

Bảng Liên Kết

TÓM TẮT

1 GIỚI THIỆU

2 LÀM PHẲNG VÀ XẤP XỈ CUNG CỦA ĐƯỜNG CONG

3 XOẮN ỐC EULER VÀ ĐƯỜNG CONG SONG SONG CỦA CHÚNG

4 ĐƯỜNG CONG SONG SONG LÀM PHẲNG

5 THƯỚC ĐO LỖI CHO XẤP XỈ BẰNG CUNG

6 EVOLUTES

7 CHUYỂN ĐỔI TỪ BÉZIER BẬC BA SANG XOẮN ỐC EULER

8 TRIỂN KHAI GPU

9 KẾT QUẢ

KẾT LUẬN, CÔNG VIỆC TƯƠNG LAI VÀ TÀI LIỆU THAM KHẢO

\

THƯỚC ĐO LỖI CHO XẤP XỈ BẰNG CUNG

Vấn đề xấp xỉ một đường cong bằng một chuỗi các đoạn cung có nhiều tài liệu nghiên cứu, nhưng không có giải pháp đã công bố nào thực sự phù hợp cho ứng dụng của chúng tôi. Vấn đề cụ thể về việc xấp xỉ một xoắn ốc Euler bằng các cung được xem xét trong Meek và Walton [2004] sử dụng phương pháp phân chia thích ứng "cắt rồi đo", nhưng giải pháp của họ có chất lượng kém; nó tỷ lệ theo 𝑂(1/𝑛 2 ), trong khi 𝑂(1/𝑛 3 ) là có thể đạt được. Kết quả đã được cải thiện "một chút" bởi Narayan [2014].

\ Tài liệu cũng chứa các kết quả tối ưu, cụ thể là Maier [2014] và Nuntawisuttiwong và Dejdumrong [2021], nhưng với chi phí đáng kể; cả hai phương pháp đều tuyên bố độ phức tạp thời gian 𝑂(𝑛 2 ). Điểm chung cho tất cả các kết quả này là họ đang giải quyết một vấn đề khó hơn: áp dụng ràng buộc rằng chuỗi cung được tạo ra là liên tục 𝐺 1 . Mặc dù mong muốn cho nhiều ứng dụng, ràng buộc này không cần thiết cho việc hiển thị đường viền nét vẽ.

\ Ngay cả khi ràng buộc này được nới lỏng, sự không liên tục về góc của một xấp xỉ cung là rất nhỏ so với việc làm phẳng thành các đường thẳng. Phương pháp của chúng tôi dựa trên một thước đo lỗi đơn giản, tương tự về bản chất với thước đo dùng cho việc làm phẳng thành các đoạn thẳng. Chi tiết của thước đo (đặc biệt là điều chỉnh các hằng số) được thu được một cách thực nghiệm, mặc dù chúng tôi nghi ngờ rằng các giới hạn phân tích nghiêm ngặt hơn có thể đạt được. Trong thực tế, nó hoạt động rất tốt; cách tốt nhất để quan sát điều đó là một công cụ kiểm tra tương tác, được cung cấp trong các tài liệu bổ sung.

Thước đo lỗi được đề xuất như sau. Lỗi khoảng cách ước tính cho một đường cong có độ dài 𝑠ˆ là:

𝑑 ≈ 1 120 ∫ 𝑠ˆ 0 3 √︁ |𝜅 ′ (𝑠)|𝑑𝑠!3

Đối với một đoạn xoắn ốc Euler, 𝜅 ′ (𝑠) là hằng số và do đó thước đo lỗi này trở nên gần như tầm thường. Với 𝑛 phân chia, khoảng cách ước tính đơn giản là 𝑠 3𝜅 ′ 120𝑛 3 . Giải cho 𝑛, chúng ta có 𝑛 = 𝑠 3 √︃ |𝜅 ′ | 120𝑑 phân chia, và những phân chia này được chia đều theo độ dài cung, vì mật độ phân chia là hằng số trên toàn bộ đường cong, giống như trường hợp làm phẳng cung thành đường thẳng. Đáng chú ý, việc xấp xỉ một đường cong song song xoắn ốc Euler bằng các đoạn cung gần như đơn giản như việc xấp xỉ xoắn ốc Euler thành các cung.

\ Như trong việc làm phẳng thành đường thẳng, tham số cho đường cong là độ dài cung của xoắn ốc Euler gốc. Mật độ phân chia sau đó là hằng số, và chỉ cần một điều chỉnh nhỏ cho công thức tính số lượng phân chia, có tính đến sự biến đổi độ cong bổ sung từ độ lệch bởi ℎ (nửa độ rộng đường). Công thức sửa đổi là:

𝑛 = 𝑠 3 √︂ |𝜅 ′ | (1 + 0.4|ℎ𝑠𝜅′ |) 120𝑑

Công thức này được xác định một cách thực nghiệm bằng cách khớp đường cong với các giá trị lỗi đo được từ việc xấp xỉ các đường cong song song xoắn ốc Euler thành các cung, nhưng cũng được lấy cảm hứng từ việc áp dụng công thức thước đo lỗi tổng quát cho các phương trình phân tích của đường cong song song xoắn ốc Euler, và bỏ qua các số hạng bậc cao hơn. Một cách dẫn xuất nghiêm ngặt hơn, lý tưởng là với các giới hạn lỗi chắc chắn, vẫn còn là công việc trong tương lai.

\ Một hệ quả của công thức này là, vì lỗi tính theo giá trị tuyệt đối của ℎ, độc lập với dấu, cùng một xấp xỉ cung có thể được sử dụng cho cả hai bên của nét vẽ. Xem Hình 8 để so sánh giữa việc làm phẳng thành đa giác và xấp xỉ với các đoạn cung. Phiên bản đoạn cung có ít đoạn hơn nhiều ở cùng một dung sai, trong khi vẫn giữ được chất lượng hình ảnh rất cao.

EVOLUTES

Trong đặc tả đúng đắn, có nguyên tắc cho việc vẽ nét [19], các đường cong song song chỉ đủ cho các đoạn mà độ cong

\

\ không vượt quá nghịch đảo nửa độ rộng. Khi nó vượt quá, các đoạn bổ sung phải được vẽ, bao gồm các evolute của đường cong gốc. Nói chung, evolute của một Bézier bậc ba là một đường cong rất phức tạp, đòi hỏi các kỹ thuật xấp xỉ. Ngược lại, evolute của một xoắn ốc Euler (𝜅 = 𝑎𝑠) là một xoắn ốc khác với một phương trình Cesàro đơn giản, cụ thể là 𝜅 = −𝑎 −1 𝑠 −3 , một ví dụ của kết quả tổng quát rằng evolute của một đường cong log-aesthetic là một đường cong log-aesthetic khác [26].

\ Làm phẳng evolute này cũng đơn giản; mật độ phân chia tỷ lệ với 𝑠 −0.5 trong đó 𝑠 là tham số độ dài cung của xoắn ốc Euler cơ bản (và được dịch chuyển sao cho 𝑠 = 0 là điểm uốn). Do đó, tích phân là 2 √ 𝑠, và tích phân nghịch đảo chỉ là bình phương. Vì vậy, làm phẳng evolute của một xoắn ốc Euler đơn giản hơn việc làm phẳng đường cong song song của nó. T

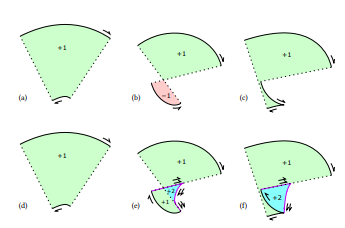
\ ác động của việc thêm evolutes để đạt được tính đúng đắn mạnh được thể hiện trong Hình 9. Các đoạn evolute bổ sung và các đường kết nối được xuất ra hai lần, để làm cho các số vòng quay nhất quán và tạo ra một đường viền kín nước. Tất cả các số vòng quay đều dương, vì vậy việc hiển thị với quy tắc vòng quay khác không cho kết quả hiển thị cuối cùng chính xác.

:::info Tác giả:

1. Raph Levien
2. Arman Uguray

:::

:::info Bài báo này có sẵn trên arxiv dưới giấy phép CC 4.0.

:::

\