Производительность оптимизации на синтетических гауссовских и древовидных встраиваниях

Таблица ссылок

Резюме и 1. Введение

1. Смежные работы

2. Техники выпуклой релаксации для гиперболических SVM

   3.1 Предварительные сведения

   3.2 Исходная формулировка HSVM

   3.3 Полуопределенная формулировка

   3.4 Момент-сумма-квадратов релаксация

3. Эксперименты

   4.1 Синтетический набор данных

   4.2 Реальный набор данных

4. Обсуждения, благодарности и ссылки

   \

A. Доказательства

B. Извлечение решения в релаксированной формулировке

C. Об иерархии момент-сумма-квадратов релаксации

D. Масштабирование Платта [31]

E. Детальные экспериментальные результаты

F. Робастная гиперболическая машина опорных векторов

4.1 Синтетический набор данных

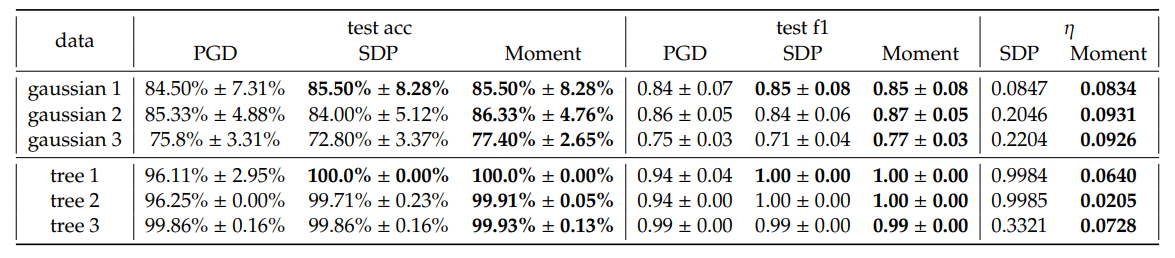
\ В целом мы наблюдаем небольшой прирост в средней точности теста и взвешенной F1 оценке для SDP и Moment относительно PGD. Примечательно, что Moment часто демонстрирует более последовательные улучшения по сравнению с SDP в большинстве конфигураций. Кроме того, Moment дает меньшие разрывы оптимальности 𝜂, чем SDP. Это соответствует нашим ожиданиям, что Moment более точен, чем SDP.

\ Хотя в некоторых случаях, например, когда 𝐾 = 5, Moment достигает значительно меньших потерь по сравнению с PGD и SDP, это обычно не так. Мы подчеркиваем, что эти потери не являются прямыми измерениями обобщаемости гиперболических разделителей с максимальным отступом; скорее, они представляют собой комбинации максимизации отступа и штрафа за неправильную классификацию, которая масштабируется с 𝐶. Таким образом, наблюдение, что производительность в точности теста и взвешенной F1 оценке лучше, хотя потери, вычисленные с использованием извлеченных решений из SDP и Moment, иногда выше, чем из PGD, может быть связано со сложным ландшафтом потерь. Более конкретно, наблюдаемые увеличения потерь можно объяснить сложностью ландшафта, а не эффективностью методов оптимизации. Основываясь на результатах точности и F1 оценки, эмпирически методы SDP и Moment определяют решения, которые обобщаются лучше, чем те, которые получены при использовании только градиентного спуска. Мы предоставляем более детальный анализ влияния гиперпараметров в Приложении E.2 и время выполнения в Таблице 4. Граница решения для Gaussian 1 визуализирована на Рисунке 5.

\

\ Синтетическое вложение дерева. Поскольку гиперболические пространства хорошо подходят для вложения деревьев, мы генерируем случайные древовидные графы и вкладываем их в H2, следуя Mishne et al. [6]. В частности, мы помечаем узлы как положительные, если они являются дочерними для указанного узла, и отрицательными в противном случае. Затем наши модели оцениваются для классификации поддеревьев с целью определения границы, которая включает все дочерние узлы в пределах одного поддерева. Такая задача имеет различные практические применения. Например, если дерево представляет набор токенов, граница решения может выделить семантические регионы в гиперболическом пространстве, которые соответствуют поддеревьям графа данных. Мы подчеркиваем, что общей особенностью такой задачи классификации поддеревьев является дисбаланс данных, который обычно приводит к плохой обобщаемости. Следовательно, мы стремимся использовать эту задачу для оценки производительности наших методов в этих сложных условиях. Три вложения выбраны и визуализированы на Рисунке 3, а производительность суммирована в Таблице 1. Время выполнения для выбранных деревьев можно найти в Таблице 4. Граница решения для дерева 2 визуализирована на Рисунке 6.

\ Подобно результатам синтетических гауссовских наборов данных, мы наблюдаем лучшую производительность SDP и Moment по сравнению с PGD, и из-за дисбаланса данных, с которым методы GD обычно испытывают трудности, мы получаем больший прирост во взвешенной F1 оценке в этом случае. Кроме того, мы наблюдаем большие разрывы оптимальности для SDP, но очень узкий разрыв для Moment, подтверждая оптимальность Moment даже при серьезном дисбалансе классов.

\

\

:::info Авторы:

(1) Sheng Yang, Школа инженерных и прикладных наук имени Джона А. Полсона, Гарвардский университет, Кембридж, Массачусетс ([e-mail]);

(2) Peihan Liu, Школа инженерных и прикладных наук имени Джона А. Полсона, Гарвардский университет, Кембридж, Массачусетс ([e-mail]);

(3) Cengiz Pehlevan, Школа инженерных и прикладных наук имени Джона А. Полсона, Гарвардский университет, Кембридж, Массачусетс, Центр наук о мозге, Гарвардский университет, Кембридж, Массачусетс, и Институт Кемпнера по изучению естественного и искусственного интеллекта, Гарвардский университет, Кембридж, Массачусетс ([e-mail]).

:::

---

:::info Эта статья доступна на arxiv под лицензией CC by-SA 4.0 Deed (Attribution-Sharealike 4.0 International).

:::

\