Здесь нет победителей: почему каждый "справедливый" криптоаукцион оказывается тривиальным

Таблица ссылок

Резюме и 1. Введение

1.1 Технический обзор

1.2 Связанные работы

1. Модель и предварительные сведения и 2.1 Механизмы комиссий за транзакции

   2.2 Желаемые свойства TFM

2. Понимание OCA

   3.1 Разница между SCP и OCA

   3.2 Полезные предварительные результаты для OCA-устойчивых TFM

3. Детерминированные OCA-устойчивые механизмы

4. Рандомизированные OCA-устойчивые механизмы

5. Обсуждение и ссылки

   \

A. Отсутствующие доказательства

B. Неанонимные детерминированные механизмы

4 Детерминированные OCA-устойчивые механизмы

Пример 3.6 показывает, что в общем случае свойства DSIC и 1-OCA-устойчивости недостаточно для гарантии нулевого дохода. Теперь мы покажем, что для детерминированных механизмов добавление свойства MMIC достаточно для получения общего результата с нулевым доходом.

\ Теорема 4.1. Каждый детерминированный DSIC+MMIC+1-OCA-устойчивый механизм имеет 0 дохода майнера.

\

\ Однако мы можем предоставить содержательную характеристику даже при удалении условия DSIC. Характеристика, приведенная в Лемме 4.3, остается очень похожей, хотя и с большей свободой в определении правила оплаты.

\

\ Мы заключаем, что сжигание для всех распределенных значений является некоторой константой R. Теперь сравним R с r, которое у нас есть для правила распределения.

\ Мы заключаем, что R = r, что дает указанную характеристику.

\ Это позволяет нам дальше характеризовать правила распределения и сжигания более обобщенно для детерминированных 1-OCA-устойчивых механизмов.

\ Лемма 4.4. Любой 1-OCA-устойчивый детерминированный механизм a, p, β имеет точно следующую форму: Для некоторого r ≥ 0 механизм распределяет предмет участнику с наивысшей ставкой при условии, что она имеет значение выше r, или не распределяет предмет вообще. При распределении сжигание равно точно r. То есть,

\

\

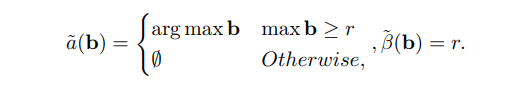
\ Теперь мы можем точно охарактеризовать два класса механизмов: класс DSIC+1-OCA-устойчивых детерминированных механизмов и класс MMIC+1-OCA-устойчивых детерминированных механизмов.

\

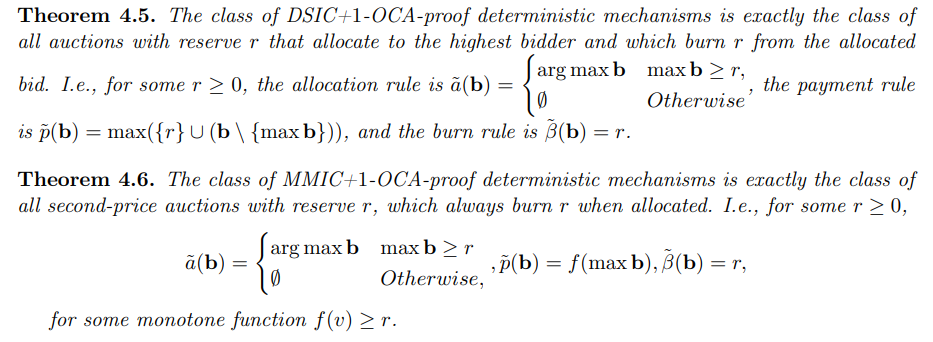
\ Эти точные характеристики теперь позволяют нам сделать следующий вывод:

Теорема 4.7. Никогда не распределять предмет - это единственный DSIC+MMIC+1-OCA-устойчивый детерминированный механизм.

\ Доказательство. Это следует из Теоремы 4.5 и Теоремы 4.6, поскольку два класса, охарактеризованные в этих результатах, имеют только тривиальный механизм общий (принимая r = ∞). Чтобы интуитивно понять это, рассмотрим класс аукционов второй цены с резервом r и постоянным сжиганием r из Теоремы 4.5. Аукционы второй цены не являются MMIC, поскольку майнер может добавить фиктивного участника произвольно близко к выигрышной ставке, чтобы увеличить платеж.

\

5 Рандомизированные OCA-устойчивые механизмы

Теперь мы расширяем обсуждение до рандомизированных OCA-устойчивых механизмов. Для рандомизированных механизмов мы рассматриваем более сильное понятие OCA-устойчивости (а не 1-OCA-устойчивости). Мы делаем это, чтобы избежать загромождения в определениях, поскольку в рандомизированных механизмах выигрышная коалиция вполне может обязательно включать всех участников торгов (поскольку каждый имеет некоторую дробную вероятность выигрыша).

\ Теперь рассмотрим естественное свойство для механизмов:

\ Следствие 5.4. По Лемме 5.3, DSIC+OCA-устойчивый масштабно-инвариантный механизм не сжигает комиссии (т.е. его правило сжигания является постоянной нулевой функцией), в то время как из Леммы 3.5 мы получаем, что DSIC+MMIC+OCA-устойчивый механизм имеет платежи, равные сжиганию в случае одного участника. Следовательно, мы должны иметь 0 платежей в случае одного участника, и поэтому в случае одного участника предмет либо всегда, либо никогда не распределяется.

\ Лемма 5.5. Для DSIC+MMIC+OCA-устойчивого механизма, если предмет всегда или никогда не распределяется в случае одного участника, механизм должен быть тривиальным.

\

\ Таким образом, как прямой результат Следствия 5.4 и Леммы 5.5, мы имеем:

Следствие 5.6. Не существует нетривиального масштабно-инвариантного DSIC+MMIC+OCA-устойчивого механизма.

\ Аргумент, который мы используем в Лемме 5.5, может быть расширен, чтобы позволить нам также исключить класс аукционов, которые удовлетворяют свойству, которое мы называем постоянной общей вероятностью распределения (CTPA), которое определено в Опр. 5.7. Это интересный класс аукционов, поскольку он включает все эффективные аукционы (которые являются частью класса постоянной общей вероятности 1 распределения), включая аукционы первой и второй цены.

\

\

\

\ и, таким образом, по условию выполнимости Ур. (1):

\ Заметим, что это левая часть Леммы 5.12, где мы рассматриваем ставки B · b, A · b. Таким образом, мы можем повторить способ, которым мы разработали Ур. (14) (для случая ставок A · b, A · b), и, рассматривая, что майнер опускает ставку B · b, получить:

\ Кроме того, для случая двух участников мы можем показать полезную верхнюю и нижнюю границы того, насколько функция должна "предпочитать" участника с более высокой ставкой:

\

\

\

\

:::info Авторы:

(1) Йотам Гафни, Институт Вейцмана ([e-mail]);

(2) Авив Яиш, Еврейский университет, Иерусалим ([e-mail]).

:::

---

:::info Эта статья доступна на arxiv под лицензией CC BY 4.0 DEED.

:::

\