WormHoleルーティングにおける近似誤差とクエリ複雑性の理解

リンク一覧

概要と1. はじめに

1.1 私たちの貢献

1.2 設定

1.3 アルゴリズム

1. 関連研究

2. アルゴリズム

   3.1 構造分解フェーズ

   3.2 ルーティングフェーズ

   3.3 WormHoleのバリエーション

3. 理論的分析

   4.1 前提条件

   4.2 内部リングの劣線形性

   4.3 近似誤差

   4.4 クエリ複雑性

4. 実験結果

   5.1 WormHole𝐸、WormHole𝐻とBiBFS

   5.2 インデックスベースの手法との比較

   5.3 基本要素としてのWormHole：WormHole𝑀

参考文献

4.3 近似誤差

Chung-Luコアを含む劣線形内部リングを持つようになったので、それを通じてルーティングパスを行うと小さなペナルティしか発生しないことを示す必要があります。直感的に言えば、内部リングが大きいほど、これを満たすのは容易になります：内部リングがグラフ全体である場合、この主張は自明に成り立ちます。したがって、課題は劣線形内部リングでも精度の面で強い保証を達成できることを示すことにあります。WormHoleはすべてのペアに対して最大𝑂(loglog𝑛)の加法的誤差しか発生しないことを証明します。これは直径Θ(log𝑛)よりもはるかに小さいです。

\

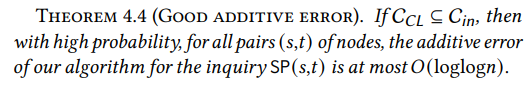
\ 上記の結果は最悪の場合でも高い確率で成り立ちます。つまり、グラフ内のすべての頂点ペア(𝑠,𝑡)に対して、WormHoleが返すパスの長さは、𝑠と𝑡の間の実際の距離よりも最大で𝑂(loglog𝑛)だけ長くなります。これは自明に、WormHoleの平均加法的誤差が高い確率で同じ量によって制限されることを意味します。

\

\

4.4 クエリ複雑性

この論文でのノードクエリモデル（§1.2参照）を思い出してください：単一のノードから始めて、反復的にクエリを行うことが許可されており、各クエリは私たちが選択したノード𝑣の隣接リストを取得します。私たちはクエリ複雑性、つまり特定の操作を実行するために必要なクエリの数に興味があります。

\ \

\ \ 最初の結果は私たちのパフォーマンスの上限です。

\ \

\ \ 証明の概略。与えられた問い合わせSP(𝑢, 𝑣)に対して、𝑢から始まるBFSのクエリ複雑性の上限を与え、同様に𝑣についても行います；総クエリ複雑性はこれら2つの量の合計です。

\ \

\ \ \

\ \ \

\ \ \

\ \ \

\ \

:::info 著者：

(1) Talya Eden、バル・イラン大学（[e-mail]）；

(2) Omri Ben-Eliezer、MIT（[e-mail]）；

(3) C. Seshadhri、UCサンタクルーズ（[e-mail]）。

:::

---

:::info この論文はarxivで入手可能であり、CC BY 4.0ライセンスの下で公開されています。

:::

\