Cómo el Algoritmo Codicioso Configura las Recompensas de los Mineros en las Redes Blockchain

Tabla de Enlaces

Abstracto y 1. Introducción

1.1 Nuestro Enfoque

1.2 Nuestros Resultados y Hoja de Ruta

1.3 Trabajos Relacionados

1. Modelo y Calentamiento y 2.1 Modelo de Blockchain

   2.2 El Minero

   2.3 Modelo de Juego

   2.4 Calentamiento: La Función de Asignación Codiciosa

2. El Caso Determinista y 3.1 Límite Superior Determinista

   3.2 La Clase de Función de Asignación Sesgada por Inmediatez

3. El Caso Aleatorizado

4. Discusión y Referencias

• A. Pruebas Faltantes para las Secciones 2, 3
• B. Pruebas Faltantes para la Sección 4
• C. Glosario

\

2.3 Modelo de Juego

Examinamos un juego entre un adversario y un minero. Esta perspectiva busca cuantificar cuántos ingresos puede perder el minero debido a su conocimiento incompleto de transacciones futuras al asignar las transacciones actualmente conocidas al próximo bloque. En este sentido, los usuarios activos en el sistema pueden considerarse como una "naturaleza" omnisciente adversaria, que crea un cronograma de transacciones del peor caso. Una función de asignación no tiene conocimiento de las transacciones futuras que serán enviadas por el adversario, por lo que la planificación óptima basada en la información parcial revelada por transacciones anteriores puede no ser el mejor curso de acción. Sin embargo, sorprendentemente, más adelante demostramos que de hecho lo es. Dada la tasa de descuento de un minero, existe una tensión conceptual entre incluir transacciones con la tarifa más alta y aquellas con el TTL más bajo. Por lo tanto, la calidad de una función de asignación x se cuantifica comparándola con la mejor función posible x′, cuando se enfrenta a un ψ adversario del peor caso. La cantidad resultante se denomina ratio competitivo de x. Para mantener la compatibilidad con la literatura sobre programación de paquetes, definimos el ratio competitivo como el mejor rendimiento offline posible dividido por el rendimiento online de una función de asignación, en lugar de al revés, por lo que tenemos Rx ≥ 1. Un límite superior se obtiene encontrando una función de asignación que garantice un buen rendimiento, y un límite inferior se obtiene demostrando que ninguna función de asignación puede garantizar un mejor rendimiento.

\ \

\ \ \

2.4 Calentamiento: La Función de Asignación Codiciosa

La función de asignación Codiciosa, definida en la Definición 2.6, es quizás un algoritmo clásico para el problema de programación de paquetes, y fue explorada por la literatura anterior para el caso no descontado. Además, la evidencia empírica sugiere que la mayoría de los mineros asignan codiciosamente las transacciones a los bloques. Trabajos anteriores muestran que en Bitcoin y Ethereum, las transacciones que pagan tarifas más altas generalmente tienen un tiempo de espera menor en el mempool, lo que significa que se incluyen relativamente rápido en los bloques [MACG20; PORH22; TFWM21; LLNZZZ22]. De hecho, los algoritmos de selección de transacciones predeterminados para Bitcoin Core (la implementación de referencia para clientes de Bitcoin) y geth (el cliente de ejecución más popular de Ethereum), priorizan las transacciones según sus tarifas, aunque el comportamiento predeterminado de ambos puede ser anulado. Por lo tanto, es de interés ver el rendimiento de este enfoque.

\ Definición 2.6 (La función de asignación Codiciosa). Dado un conjunto de transacciones S, la función de asignación Codiciosa elige la transacción de mayor pago presente en el conjunto S, sin tener en cuenta el TTL:

\

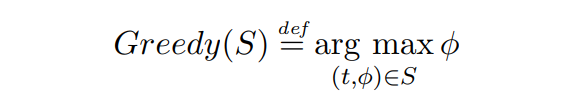
\ En caso de que haya múltiples transacciones con la misma tarifa, se prefieren aquellas con el TTL más bajo.

\ En el Ejemplo 2.7, ilustramos cómo el rendimiento de Codiciosa puede depender de la tasa de descuento.

\ Ejemplo 2.7. Examinamos el rendimiento de Codiciosa dado el siguiente adversario ψ.

\

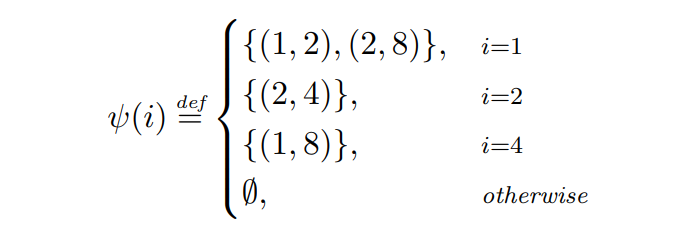
\ El cronograma de transacciones definido por ψ se muestra en la Fig. 1. En el turno 1, el adversario transmite dos transacciones: (1, 2) que expira al final del turno y tiene una tarifa de 2, y (2, 4) que paga una tarifa igual a 4 y expira al final del siguiente turno. Debido a que Codiciosa prioriza las transacciones con tarifas más altas, asignará (2, 4), mientras deja que la otra transacción expire. En el siguiente turno, el adversario transmite una única transacción con un TTL de 2 y una tarifa de 6, que es la única disponible para Codiciosa en ese turno, y por lo tanto será asignada. En el paso 3, el adversario no emite ninguna transacción, y en el paso 4, se transmite una transacción (1, 8) y luego es asignada por Codiciosa.

\

\

\ En el Lema 2.8, limitamos el ratio competitivo de Codiciosa, como función de la tasa de descuento.

\

\

\

\

:::info Autores:

(1) Yotam Gafni, Instituto Weizmann ([e-mail]);

(2) Aviv Yaish, Universidad Hebrea, Jerusalén ([e-mail]).

:::

---

:::info Este artículo está disponible en arxiv bajo la licencia CC BY 4.0 DEED.

:::

\