ExchangeDEX+

Buy Crypto Markets Spot Futures500X Earn Events

Gold Bar & BTC Giveaway2000g

Los fractales son patrones infinitos creados por ecuaciones matemáticas repetitivas. Dibujaremos uno de los fractales más conocidos, utilizando solo JavaScript puro y la API de Canvas HTML5.Los fractales son patrones infinitos creados por ecuaciones matemáticas repetitivas. Dibujaremos uno de los fractales más conocidos, utilizando solo JavaScript puro y la API de Canvas HTML5.

Codificando un Árbol Fractal con JavaScript y HTML5

Autor: Hackernoon

2025/10/11 03:00

TREE$0.1146-3.45%

LL$0.007617-3.82%

\ Fractales, esas figuras enigmáticas que están en todas partes pero no pueden ser vistas por el ojo inexperto. Hoy dibujaremos uno de los Fractales más conocidos, usando solo Vanilla JS y la API de Canvas HTML5. ¡Vamos a programar!

Lo que aprenderás

¿Qué es un Árbol Fractal?
Escribiendo el Árbol Fractal en Vanilla JS
Más allá del Árbol Fractal

¿Qué es un Árbol Fractal?

Para definir un Árbol Fractal, primero debemos conocer la definición de Fractal, por supuesto.

Los Fractales son patrones infinitos creados por ecuaciones matemáticas repetitivas, que, en cualquier escala, en cualquier nivel de zoom, se ven aproximadamente iguales. En otras palabras, un objeto geométrico cuya estructura básica, áspera o fragmentada, se repite a sí misma en diferentes escalas.

Así que si dividimos un Fractal, veremos una copia reducida del todo.

Benoit Mandelbrot, quien acuñó el término Fractal en 1975, dijo:

\ Bastante claro, ¿verdad?

Aquí hay algunos ejemplos:

Animated Von Koch Curve

\ Animated Sierpinski Carpet

Ahora, ¿qué es un Árbol Fractal?

Imagina una rama, y ramas saliendo de ella, y luego dos ramas saliendo de cada rama, y así sucesivamente... así es como se ve un Árbol Fractal.

Su forma proviene del triángulo de Sierpinski (o junta de Sierpinski).

Como puedes ver, uno se convierte en el otro al cambiar el ángulo entre las ramas:

From Sierpinski Triangle to Fractal

Hoy, terminaremos con una figura similar a la forma final de ese GIF.

Escribiendo el Árbol Fractal en Vanilla JS

En primer lugar, aquí está el producto final (puedes ajustarlo a lo largo del camino):

Final Fractal Tree

Ahora vamos a dibujarlo, paso a paso.

Primero, inicializamos nuestro archivo index.html con un canvas de dimensiones razonables y una etiqueta script donde estará todo nuestro código JS.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script></script>   </body> </html>

Luego, comenzamos a escribir nuestro JavaScript.

Inicializamos nuestro elemento canvas en JS, accediendo a él a través de la variable myCanvas y creando el contexto de renderizado 2D con la variable ctx (contexto).

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");     </script>   </body> </html>

Así que sí, el método getContext agrega propiedades y métodos que te permiten dibujar, en este caso, en 2D.

Ahora es momento de pensar. ¿Cómo podemos definir el algoritmo para dibujar un árbol Fractal? Hmm... 🤔

Veamos, sabemos que las ramas se vuelven cada vez más pequeñas. Y que cada rama termina con dos ramas saliendo de ella, una a la izquierda y otra a la derecha.

En otras palabras, cuando una rama es lo suficientemente larga, adjunta dos ramas más pequeñas a ella. Repetir.

Suena como si deberíamos usar alguna declaración recursiva en algún lugar, ¿no es así?

Volviendo al código, ahora definimos nuestra función fractalTree que debería tomar al menos cuatro argumentos: las coordenadas X e Y donde comienza la rama, la longitud de su rama y su ángulo.

Dentro de nuestra función, comenzamos el dibujo con el método beginPath(), y luego guardamos el estado del canvas con el método save().

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle) {           ctx.beginPath();           ctx.save();       }     </script>   </body> </html>

El método beginPath se usa a menudo cuando comienzas una nueva línea o figura que tiene un estilo fijo, como el mismo color a lo largo de toda la línea, o el mismo ancho. El método save simplemente guarda todo el estado del canvas empujando el estado actual a una pila.

Ahora dibujaremos nuestro Árbol Fractal dibujando una línea (rama), rotando el canvas, dibujando la siguiente rama, y así sucesivamente. Va así (explicaré cada método debajo del ejemplo de código):

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle) {           ctx.beginPath();           ctx.save();            ctx.translate(startX, startY);           ctx.rotate(angle * Math.PI/180);           ctx.moveTo(0, 0);           ctx.lineTo(0, -len);           ctx.stroke();            if(len < 10) {               ctx.restore();               return;           }            draw(0, -len, len*0.8, -15);           draw(0, -len, len*0.8, +15);            ctx.restore();       }       draw(400, 600, 120, 0)     </script>   </body> </html>

Así que primero agregamos tres métodos, translate, rotate y moveTo, que "mueven" el canvas, su origen y nuestro "lápiz" para que podamos dibujar la rama en el ángulo deseado. Es como si estuviéramos dibujando una rama, luego centrando esta rama (moviendo todo el canvas), y luego dibujando una nueva rama desde el final de nuestra rama anterior.

Los últimos dos métodos antes de la declaración if son lineTo y stroke; el primero agrega una línea recta a la ruta actual, y el segundo la renderiza. Puedes pensar en ello así: lineTo da la orden, y stroke la ejecuta.

Ahora tenemos una declaración if que indica cuándo detener la recursión, cuándo dejar de dibujar. El método restore, como se indica en los Docs de MDN, "restaura el estado del canvas guardado más recientemente sacando la entrada superior de la pila de estado de dibujo".

Después de la declaración if, tenemos la llamada recursiva y otra llamada al método restore. Y luego una llamada a la función que acabamos de terminar.

Ahora ejecuta el código en tu navegador. ¡Verás, finalmente, un Árbol Fractal!

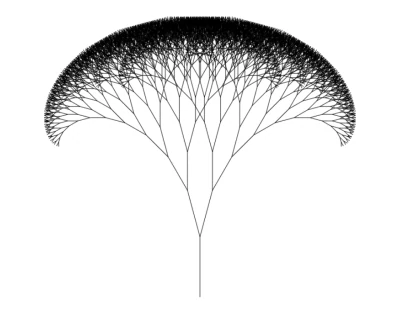
Fractal Tree First Iteration

Impresionante, ¿verdad? Ahora hagámoslo aún mejor.

Agregaremos un nuevo parámetro a nuestra función draw, branchWidth, para hacer nuestro Árbol Fractal más realista.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle, branchWidth) {           ctx.lineWidth = branchWidth;            ctx.beginPath();           ctx.save();            ctx.translate(startX, startY);           ctx.rotate(angle * Math.PI/180);           ctx.moveTo(0, 0);           ctx.lineTo(0, -len);           ctx.stroke();            if(len < 10) {               ctx.restore();               return;           }            draw(0, -len, len*0.8, angle-15, branchWidth*0.8);           draw(0, -len, len*0.8, angle+15, branchWidth*0.8);            ctx.restore();       }       draw(400, 600, 120, 0, 10)     </script>   </body> </html>

Así que en cada iteración, estamos haciendo cada rama más delgada. También he cambiado el parámetro de ángulo en la llamada recursiva para hacer un árbol más "abierto".

Ahora, ¡agreguemos algo de color! Y sombras, por qué no.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle, branchWidth) {           ctx.lineWidth = branchWidth;            ctx.beginPath();           ctx.save();            ctx.strokeStyle = "green";           ctx.fillStyle = "green";            ctx.translate(startX, startY);           ctx.rotate(angle * Math.PI/180);           ctx.moveTo(0, 0);           ctx.lineTo(0, -len);           ctx.stroke();            ctx.shadowBlur = 15;           ctx.shadowColor = "rgba(0,0,0,0.8)";            if(len < 10) {               ctx.restore();               return;           }            draw(0, -len, len*0.8, angle-15, branchWidth*0.8);           draw(0, -len, len*0.8, angle+15, branchWidth*0.8);            ctx.restore();       }       draw(400, 600, 120, 0, 10)     </script>   </body> </html>

Ambos métodos de color son autoexplicativos (strokeStyle y fillStyle). También, los de sombra, shadowBlur y shadowColor.

¡Y eso es todo! Guarda el archivo y ábrelo con tu navegador para ver el producto final.

¡Ahora te animo a jugar con el código! Cambia el shadowColor, el fillStyle, haz un Árbol Fractal más corto o más largo, cambia el ángulo, o intenta agregar hojas, eso debería ser desafiante 😉

Más allá del Árbol Fractal

Como te mostré al principio de esta publicación, hay diferentes Fractales. No va a ser fácil hacer todos esos con la API de Canvas, pero debería ser posible. Hice algunos de esos en el lenguaje de programación C, y también he jugado con p5.js.

p5.js es una biblioteca JavaScript de código abierto hecha por artistas, para artistas, basada en el lenguaje Processing. Puedes dibujar o animar cualquier cosa imaginable. Si estás interesado en hacer arte con código, es imprescindible. Tienen una gran página de inicio que puedes consultar aquí.

¡Bueno, eso es todo por ahora! Gracias por leer, comenta cualquier pregunta, ¡y nos vemos en mi próxima publicación!

Aviso legal: Los artículos republicados en este sitio provienen de plataformas públicas y se ofrecen únicamente con fines informativos. No reflejan necesariamente la opinión de MEXC. Todos los derechos pertenecen a los autores originales. Si consideras que algún contenido infringe derechos de terceros, comunícate a la dirección service@support.mexc.com para solicitar su eliminación. MEXC no garantiza la exactitud, la integridad ni la actualidad del contenido y no se responsabiliza por acciones tomadas en función de la información proporcionada. El contenido no constituye asesoría financiera, legal ni profesional, ni debe interpretarse como recomendación o respaldo por parte de MEXC.