The Dark Side of Deterministic Signatures

Table of Links

Abstract and I. Introduction

II. Edwards-Curve Digital Signature Algorithm

III. Double Public Key Signing Function Oracle Attack

IV. Countermeasures

V. Conclusion and References

II. EDWARDS-CURVE DIGITAL SIGNATURE ALGORITHM

EdDSA is a digital signature algorithm similar to ECDSA [4] proposed by Bernstein et al. [11]. RFC 8032 [14] defines EdDSA defines for two twisted Edwards curves Ed25519 (similar to curve25519 proposed by Bernstein [10]) and Ed448; however, EdDSA may be instantiated over other curves. For a fixed field k, a twisted Edwards curve with the coefficients a, d ∈ k is the curve:

\

\ The sum of two points in the Ed25519 and Ed448 curves is represented by the following addition rule:

\

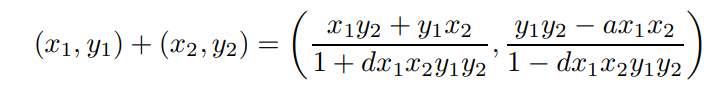
\ where the point (0, 1) is the neutral element. The above rule can also be used for point doubling and addition. Adding a point P to itself n times is the same as multiplication by a scalar, denoted as n · P.

\

\

\ A. EdDSA Signing

\

\ The signature (R, S) of a message m ∈ {0, 1} ∗ is computed according to Algorithm 1. A significant difference between EdDSA and ECDSA is the signature generated is deterministic in EdDSA; in other words, for a message, any signature computed using the same key pair and public parameters will always be the same.

\

\ B. EdDSA Signature Verification

\ The EdDSA verification algorithm given in Algorithm 2 generally conforms to both the RFC 8032 standard and [14], and the NIST FIPS 186-5 standard [15], while also providing the strongest notion of security defined by Brendel et al. [17] and Chalkias et al. [18]: Strong UnForgeability under Chosen Message Attacks (SUF-CMA) with Strongly Binding Signatures (SBS). This means that efficient adversaries cannot output valid signatures on new messages nor find a new signature for old messages. Furthermore, messages are bound to the public key, a property shown to be lacking in the RFC 8032 variant of EdDSA [17].

\

\

\

\ Verification of an EdDSA signature can be done either cofactored or cofactorless. The verification described by Algorithm 2 is cofactored. If the implementation uses cofactorless implementation, then it is required to reduce H(R || pk || m) to the range [0, ℓ) before multiplication by pk. Not doing so may cause implementations to disagree on the validity of signatures generated by mixed-order public keys. When performing cofactored verification, multiplication by c should be performed as a separate scalar-by-point multiplication. Failing to ensure separate scalar-by-point multiplication can cause the result in c·H(R || pk || m) mod ℓ not being divisible by c and thus, not clear the low order component in pk if it exists. While Bernstein et al. [11] originally proposed to use cofactorless verification, EdDSA standards recommend using the cofactored verification algorithm [14], [15].

\

III. DOUBLE PUBLIC KEY SIGNING FUNCTION ORACLE ATTACK

The discovered vulnerability takes the form of an oracle attack. The oracle uses the signing function of a deterministic signature scheme with a fixed secret key and message parameters to compute a signature given an arbitrary public key. If given access to this type of oracle, an adversary can use it to recover the secret key by submitting two different public keys. In this section, an attack methodology is described, and a list of affected libraries and their current status on fixing the issue is given.

\ A. Attacking EdDSA

\ According to both the RFC 8032 [14] and FIPS 186-5 [15] standards, EdDSA signatures are deterministic. This means that for the same message m ∈ {0, 1} ∗ input to a signing function with public key pk and secret key sk, a unique signature (R, S) is generated. An important detail of the signing function given in Algorithm 1 is that the signer’s public key is used in the deterministic computation of the scalar value S but not the point on the curve R in the signature (R, S). The implication of this is that if an adversary was able to use the signing function as an oracle that expects arbitrary public key inputs, they could compute two signatures (R, S) and (R, S′ ) corresponding to the same m.

\

2.1 The adversary computes e := H(R || pk || m) and e ′ := H(R || pk′ || m).

\ 2.2 Because S = r + e · s (mod ℓ) and S ′ = r + e ′ · s (mod ℓ), subtracting S′ from S gives the following

\ S − S ′ = r + e · s − r + e ′ · s (mod ℓ)

= e · s − e ′ · s (mod ℓ)

= s · (e − e ′ ) (mod ℓ)

\ 2.3 Dividing S − S ′ through by e − e ′ to recovers the value

\ s = (S − S ′ )(e − e ′ ) −1 (mod ℓ)

\

c · S · G = c · (r + H(R || pk || m) · s) · G

= c · R + c · H(R || pk || m) · s · G

= c · R + c · H(R || pk || m) · pk

\ meaning the verification algorithm still holds. Therefore, it is still possible to sign arbitrary messages, effectively breaking the SUF-CMA security with the SBS notion of security that EdDSA guarantees.

\ B. Vulnerable Libraries

\ There are a huge number of software implementations of EdDSA across many different languages. To give an idea of how common this vulnerability can be, a table of vulnerable libraries can be seen in Table II. Most of these libraries are taken from the IANIX list of “Things that use Ed25519” [26]. These libraries have been notified of the issues, and their current status of fixing the vulnerability at the time of publication is included in the table [1].

\

:::info Authors:

(1) Sam Grierson, Blockpass ID Lab, Edinburgh Napier University, Edinburgh, UK ([e-mail]);

(2) Konstantinos Chalkias, Mysten Labs Research;

(3) William J Buchanan, Blockpass ID Lab, Edinburgh Napier University, Edinburgh, UK ([e-mail]);

(4) Leandros Maglaras, Blockpass ID Lab, Edinburgh Napier University, Edinburgh, UK ([e-mail]).

:::

---

:::info This paper is available on arxiv under CC BY 4.0 DEED license.

:::

[1] A comprehensive list of libraries and requested fixes can be found here: https://github.com/MystenLabs/ed25519-unsafe-libs