Fractal Geometry as the Blueprint for Encryption

:::info Authors:

(1) Jacques Peyriere, Engineering Research Center of Ministry of Education for Financial Computing and Digital Engineering, Renmin University of China, Beijing, 100872, P. R. China and Institut de Mathematiques d’Orsay, CNRS, Universite Paris-Saclay, 91405 Orsay, France;

(2) Fengxia Liu (Corresponding author), Institute of Artificial Intelligence, Beihang University, Beijing, 100191, P. R. China and Beijing Advanced Innovation Center for Future Blockchain and Privacy Computing, Beijing, P. R. China ([e-mail]);

(3) Zhiyong Zheng, Engineering Research Center of Ministry of Education for Financial Computing and Digital Engineering, Renmin University of China, Beijing, 100872, P. R. China;

(4) Zixian Gong, Engineering Research Center of Ministry of Education for Financial Computing and Digital Engineering, Renmin University of China, Beijing, 100872, P. R. China.

:::

Table of Links

Abstract and 1. Introduction

1. First protocol: Affine cryptosystems

   2.1 Preliminaries and notation

   2.2 An example

   2.3 A general framework

2. Second protocol: Projective cryptosystems

   3.1 Preliminaries

   3.2 Cryptosystems

3. Message authentication and integrity and References

Abstract

1 Introduction

\ The IFS have been introduced by Hutchinson [1] to rationalize several preexisting constructions of fractal sets and measures having some self-similarity properties. This formalism has been adopted by the fractalists’ community and gave rise to an abundant literature. Subsequently this formalism has been further developed by Mauldin and Williams [2] by the so called “Graph directed constructions”.

\

\ Several separation conditions have been defined for IFS which aimed at computing or estimating the Hausdorff dimension of the limit set of the said IFS. This is not our present goal and the separation condition we consider does not coincide with the previous ones, although the closest one is the so-called “strong separation condition”. Indeed the system (x/2, 1 − x/2) satisfies our condition on the interval [0, 1) and also on the interval (0, 1], while it satisfies on [0, 1] the “open set separation condition” which is important un fractal geometry. But for our purpose, this is our definition which is meaningful. And in the sequel, when we say that a system satisfies (or has, or fulfills) a separation condition this means that there exists an S = (S; S0, S1, . . . , Sν) as in definition 1.

\ When we have an IFS we can consider the following two problems which are closely related and which are easily solved when this IFS satisfies a separation properties.

\

\

\ The main difference between these problems is that the length of the unknown word w is not specified in the second one.

\ To get a cryptosystem from an IFS f with the separation condition, the strategy is to construct by some scrambling method a set of functions g = (g0, g1, . . . , gν−1) related to f but not obviously fulfilling a separation condition. This strategy will be developed in the next sections.

\ The graph directed constructions give rise to more complex systems of iteration of functions. In the same way as the ones described below they can give rise to cryptosystems, but we will not elaborate on this subject.

\

2.1 Preliminaries and notation

\

\

2.2 An example

\

\

\

\

1. The decoding fails, and Alice knows that the cryptogram has been tampered with.

   \

2. The decoding works for n steps. Then the cryptogram is wrongly deciphered and Alice is not aware of it.

\

2.3 A general framework

2.3.1 Remark

\ Of course, one can use systems of affine maps in higher dimension.

3.1 Preliminaries

Projective spaces and homographies

Projective IFS

In case when this IFS fulfills a separation condition the following problem is easy to solve.

\

3.2 Cryptosystems

Now we consider a set A = (A0, A1, . . . , Aν−1) of invertible (d + 1) × (d + 1)- matrices with integer entries which defines a homographic IFS fulfilling the separation condition on some S. We may suppose that the coefficients of eachs Aj have no common factor.

\ Key generation

Encryption

\ The message to be transmitted is a word w of length k ≤ n on the alphabet {0, 1, 2, . . . , ν − 1}. The corresponding cryptogram is the matrix

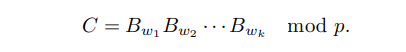
Decryption

\

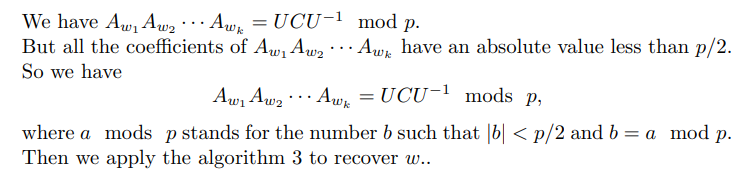
Remarks

\

\

4 Message authentication and integrity

Now Alice wants to make sure that the message supposedly coming from Bob actually comes from him. They may use the following procedure. Both Alice and Bob will use the second protocol. They share n and p and the dimension k + 1 of the matrices. Alice has already chosen a projective IFS with the separation condition whose keys are

\ (n, p, B) and (n, p, A, U, S)

\ Bob has already prepared the cryptogram C to be transmitted. In his turn he sets up an IFS with matrices of the same dimension of Alice’s. His keys are

\ (n′,p, B′) and (n′,p,A′,U′,S′).

1

References

[1] Hutchinson J.E, Fractals and self similarity, Indiana Univ. Math. J. 130 (1981), 713–747.

\ [2] Mauldin R.D. and Williams S.C., Hausdorff dimension in graph directed constructions, Trans. Amer. Math. Soc. 309 (1988), 811–829.

:::info This paper is available on arxiv under CC BY 4.0 DEED license.

:::

\