Ablation Study Confirms Necessity of Dynamic Rates for RECKONING Performance

Table of Links

Abstract and 1. Introduction

1. Background

2. Method

3. Experiments

   4.1 Multi-hop Reasoning Performance

   4.2 Reasoning with Distractors

   4.3 Generalization to Real-World knowledge

   4.4 Run-time Analysis

   4.5 Memorizing Knowledge

4. Related Work

5. Conclusion, Acknowledgements, and References

\ A. Dataset

B. In-context Reasoning with Distractors

C. Implementation Details

D. Adaptive Learning Rate

E. Experiments with Large Language Models

D Adaptive Learning Rate

Prior works [3, 4] show that a fixed learning rate shared across steps and parameters does not benefit the generalization performance of the system. Instead, [3] recommends learning a learning rate for

\

\

\ each network layer and each adaptation step in the inner loop. The layer parameters can learn to adjust the learning rates dynamically at each step. To control the learning rate α in the inner loop adaptively, we define α as a set of adjustable variable: α = {α0, α1, …αL}, where L is the number of layers and for every l = 0, …, L, αl is a vector with N elements given a pre-defined inner loop step number N. The inner loop update equation then becomes

\

\

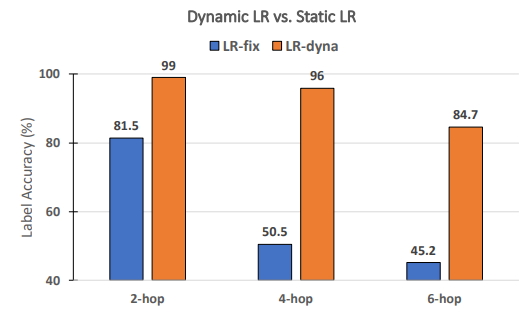
\ Are dynamic learning rates necessary for RECKONING’s performance? Following prior works on meta-learning [3, 4], we dynamically learn a set of per-step-per-layer learning rates for RECKONING. In this ablation study, we analyze whether dynamic learning rates for the inner loop effectively improve the outer loop reasoning performance. Similarly, we fix other experimental settings and set the number of inner loop steps to 4. As Figure 8 shows, when using a static learning rate (i.e., all layers and inner loop steps share a constant learning rate), the performance drops by a large margin (average drop of 34.2%). The performance drop becomes more significant on questions requiring more reasoning hops (45.5% drop for 4-hop and 39.5% drop for 6-hop), demonstrating the importance of using a dynamic learning rate in the inner loop of our framework.

\

\

:::info Authors:

(1) Zeming Chen, EPFL ([e-mail]);

(2) Gail Weiss, EPFL ([e-mail]);

(3) Eric Mitchell, Stanford University ([e-mail])';

(4) Asli Celikyilmaz, Meta AI Research ([e-mail]);

(5) Antoine Bosselut, EPFL ([e-mail]).

:::

---

:::info This paper is available on arxiv under CC BY 4.0 DEED license.

:::

\