The Role of Mutation Path Algorithms in Tree-Diffusion Program Synthesis

Table of Links

Abstract and 1. Introduction

1. Background & Related Work

2. Method

   3.1 Sampling Small Mutations

   3.2 Policy

   3.3 Value Network & Search

   3.4 Architecture

3. Experiments

   4.1 Environments

   4.2 Baselines

   4.3 Ablations

4. Conclusion, Acknowledgments and Disclosure of Funding, and References

   \

Appendix

A. Mutation Algorithm

B. Context-Free Grammars

C. Sketch Simulation

D. Complexity Filtering

E. Tree Path Algorithm

F. Implementation Details

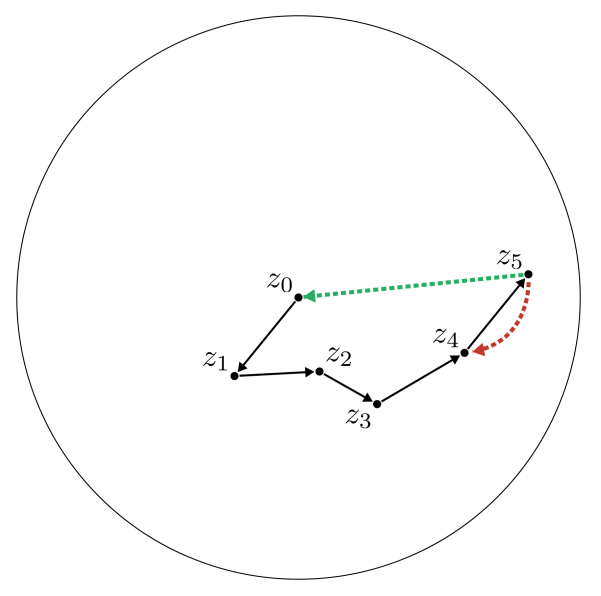
E Tree Path Algorithm

Algorithm 1 shows the high-level pseudocode for how we find the first step of mutations to transform tree A into tree B. We linearly walk down both trees until we find a node that is different. If the target node is small, i.e., its σ(z) ≤ σsmall, then we can simply mutate the source to the target. If the target node is larger, we sample a random small expression with the correct production rule, and compute the path from this small expression to the target. This gives us the first step to convert the source node to the target node. Repeatedly using Algorithm 1 gives us the full path to convert one expression to another. We note that this path is not necessarily the optimal path, but a valid path that is less noisy than the path we would get by simply chasing the last random mutation.

\

\

\

\

:::info Authors:

(1) Shreyas Kapur, University of California, Berkeley ([e-mail]);

(2) Erik Jenner, University of California, Berkeley ([e-mail]);

(3) Stuart Russell, University of California, Berkeley ([e-mail]).

:::

---

:::info This paper is available on arxiv under CC BY-SA 4.0 DEED license.

:::

\