Comment l'Algorithme Glouton Façonne les Récompenses des Mineurs dans les Réseaux Blockchain

Table des liens

Abstrait et 1. Introduction

1.1 Notre approche

1.2 Nos résultats et feuille de route

1.3 Travaux connexes

1. Modèle et échauffement et 2.1 Modèle de Blockchain

   2.2 Le Mineur

   2.3 Modèle de jeu

   2.4 Échauffement : La fonction d'allocation Greedy

2. Le cas déterministe et 3.1 Borne supérieure déterministe

   3.2 La classe de fonctions d'allocation biaisée par l'immédiateté

3. Le cas randomisé

4. Discussion et références

• A. Preuves manquantes pour les sections 2, 3
• B. Preuves manquantes pour la section 4
• C. Glossaire

\

2.3 Modèle de jeu

Nous examinons un jeu entre un adversaire et un mineur. Cette perspective vise à quantifier la perte de revenus que le mineur peut subir en raison de sa connaissance incomplète des transactions futures lors de l'allocation des transactions actuellement connues au prochain bloc. À cet égard, les utilisateurs actifs dans le système peuvent être considérés comme une "nature" omnisciente et adversariale, qui crée un calendrier de transactions dans le pire des cas. Une fonction d'allocation n'a aucune connaissance des transactions futures qui seront envoyées par l'adversaire, et donc une planification optimale basée sur les informations partielles révélées par les transactions précédentes peut ne pas être la meilleure ligne de conduite. Cependant, de façon quelque peu surprenante, nous montrons plus tard que c'est en fait le cas. Étant donné le taux d'actualisation d'un mineur, il existe une tension conceptuelle entre l'inclusion des transactions avec les frais les plus élevés et celles avec le TTL le plus bas. Ainsi, la qualité d'une fonction d'allocation x est quantifiée en la comparant à la meilleure fonction possible x′, face à un ψ adversarial dans le pire des cas. La quantité résultante est appelée le ratio compétitif de x. Pour rester compatible avec la littérature sur la planification des paquets, nous définissons le ratio compétitif comme la meilleure performance hors ligne possible divisée par la performance en ligne d'une fonction d'allocation, plutôt que l'inverse, et donc nous avons Rx ≥ 1. Une borne supérieure est alors atteinte en trouvant une fonction d'allocation qui garantit de bonnes performances, et une borne inférieure est atteinte en montrant qu'aucune fonction d'allocation ne peut garantir de meilleures performances.

\ \

\ \ \

2.4 Échauffement : La fonction d'allocation Greedy

La fonction d'allocation Greedy, définie dans la Définition 2.6, est peut-être un algorithme classique pour le problème de planification des paquets, et a été explorée par la littérature précédente pour le cas non actualisé. De plus, des preuves empiriques suggèrent que la plupart des mineurs allouent avidement les transactions aux blocs. Des travaux antérieurs montrent que dans Bitcoin et Ethereum, les transactions payant des frais plus élevés ont généralement un temps d'attente plus court dans le mempool, ce qui signifie qu'elles sont incluses relativement rapidement dans les blocs [MACG20; PORH22; TFWM21; LLNZZZ22]. En effet, les algorithmes de sélection de transactions par défaut pour Bitcoin Core (l'implémentation de référence pour les clients Bitcoin) et geth (le client d'exécution le plus populaire d'Ethereum), priorisent les transactions en fonction de leurs frais, bien que le comportement par défaut des deux puisse être remplacé. Il est donc intéressant de voir les performances de cette approche.

\ Définition 2.6 (La fonction d'allocation Greedy). Étant donné un ensemble de transactions S, la fonction d'allocation Greedy choisit la transaction la mieux rémunérée présente dans l'ensemble S, sans tenir compte du TTL :

\

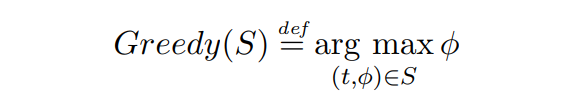
\ Dans le cas où il y a plusieurs transactions avec les mêmes frais, celles avec le TTL le plus bas sont préférées.

\ Dans l'Exemple 2.7, nous illustrons comment la performance de Greedy peut dépendre du taux d'actualisation.

\ Exemple 2.7. Nous examinons la performance de Greedy étant donné l'adversaire ψ suivant.

\

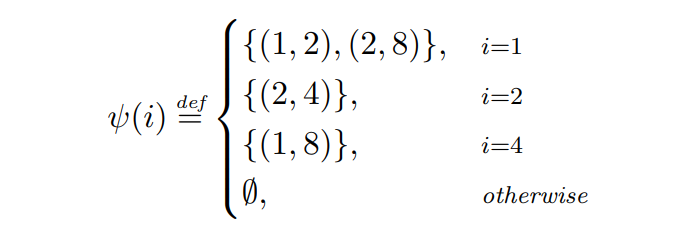
\ Le calendrier de transactions défini par ψ est représenté dans la Fig. 1. Au tour 1, l'adversaire diffuse deux transactions : (1, 2) qui expire à la fin du tour et a des frais de 2, et (2, 4) qui paie des frais égaux à 4 et expire à la fin du tour suivant. Comme Greedy priorise les transactions avec des frais plus élevés, il allouera (2, 4), tout en laissant l'autre transaction expirer. Au tour suivant, l'adversaire diffuse une seule transaction avec un TTL de 2 et des frais de 6, qui est la seule disponible pour Greedy à ce tour, et sera donc allouée. À l'étape 3, l'adversaire n'émet aucune transaction, et à l'étape 4, une transaction (1, 8) est diffusée puis allouée par Greedy.

\

\

\ Dans le Lemme 2.8, nous bornons le ratio compétitif de Greedy, en fonction du taux d'actualisation.

\

\

\

\

:::info Auteurs :

(1) Yotam Gafni, Institut Weizmann ([e-mail]);

(2) Aviv Yaish, L'Université Hébraïque, Jérusalem ([e-mail]).

:::

---

:::info Cet article est disponible sur arxiv sous licence CC BY 4.0 DEED.

:::

\