Wie der Greedy-Algorithmus die Miner-Belohnungen in Blockchain-Netzwerken gestaltet

Tabelle der Links

Abstrakt und 1. Einleitung

1.1 Unser Ansatz

1.2 Unsere Ergebnisse & Fahrplan

1.3 Verwandte Arbeiten

1. Modell und Aufwärmphase und 2.1 Blockchain-Modell

   2.2 Der Miner

   2.3 Spielmodell

   2.4 Aufwärmphase: Die Greedy-Zuweisungsfunktion

2. Der deterministische Fall und 3.1 Deterministische Obergrenze

   3.2 Die unmittelbarkeitsverzerrte Klasse von Zuweisungsfunktionen

3. Der randomisierte Fall

4. Diskussion und Referenzen

• A. Fehlende Beweise für Abschnitte 2, 3
• B. Fehlende Beweise für Abschnitt 4
• C. Glossar

\

2.3 Spielmodell

Wir untersuchen ein Spiel zwischen einem Gegner und einem Miner. Diese Perspektive zielt darauf ab zu quantifizieren, wie viel Einnahmen der Miner durch sein unvollständiges Wissen über zukünftige Transaktionen verlieren kann, wenn er die aktuell bekannten Transaktionen dem kommenden Block zuweist. In dieser Hinsicht können die im System aktiven Benutzer als eine gegnerische allwissende "Natur" betrachtet werden, die einen Worst-Case-Transaktionsplan erstellt. Eine Zuweisungsfunktion hat keine Kenntnis von zukünftigen Transaktionen, die vom Gegner gesendet werden, und so ist eine optimale Planung auf Basis der Teilinformationen, die durch vorherige Transaktionen offenbart werden, möglicherweise nicht der beste Handlungsweg. Überraschenderweise zeigen wir jedoch später, dass dies tatsächlich der Fall ist. Angesichts der Diskontrate eines Miners gibt es eine konzeptionelle Spannung zwischen der Einbeziehung von Transaktionen mit der höchsten Gebühr und denen mit der niedrigsten TTL. Die Qualität einer Zuweisungsfunktion x wird daher quantifiziert, indem sie mit der bestmöglichen Funktion x′ verglichen wird, wenn sie mit einem Worst-Case-Gegner ψ konfrontiert wird. Die resultierende Größe wird als Wettbewerbsverhältnis von x bezeichnet. Um mit der Literatur zur Paketplanung kompatibel zu bleiben, definieren wir das Wettbewerbsverhältnis als die bestmögliche Offline-Leistung geteilt durch die Online-Leistung einer Zuweisungsfunktion, anstatt umgekehrt, und so haben wir Rx ≥ 1. Eine Obergrenze wird dann erreicht, indem eine Zuweisungsfunktion gefunden wird, die eine gute Leistung garantiert, und eine Untergrenze wird erreicht, indem gezeigt wird, dass keine Zuweisungsfunktion eine bessere Leistung garantieren kann.

\ \

\ \ \

2.4 Aufwärmphase: Die Greedy-Zuweisungsfunktion

Die Greedy-Zuweisungsfunktion, definiert in Definition 2.6, ist vielleicht ein klassischer Algorithmus für das Paketplanungsproblem und wurde in der vorherigen Literatur für den nicht diskontierten Fall untersucht. Darüber hinaus deuten empirische Beweise darauf hin, dass die meisten Miner Transaktionen gierig Blöcken zuweisen. Frühere Arbeiten zeigen, dass in Bitcoin und Ethereum Transaktionen mit höheren Gebühren im Allgemeinen eine geringere Wartezeit im Mempool haben, was bedeutet, dass sie relativ schnell in Blöcke aufgenommen werden [MACG20; PORH22; TFWM21; LLNZZZ22]. Tatsächlich priorisieren die Standard-Transaktionsauswahlalgorithmen für Bitcoin Core (die Referenzimplementierung für Bitcoin-Clients) und geth (Ethereums beliebtester Ausführungsclient) Transaktionen basierend auf ihren Gebühren, obwohl das Standardverhalten beider überschrieben werden kann. Es ist daher von Interesse, die Leistung dieses Ansatzes zu sehen.

\ Definition 2.6 (Die Greedy-Zuweisungsfunktion). Gegeben eine Transaktionsmenge S wählt die Greedy-Zuweisungsfunktion die höchstzahlende Transaktion in der Menge S aus, ohne Rücksicht auf TTL:

\

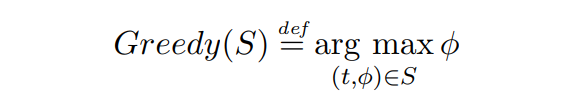
\ Falls es mehrere Transaktionen mit der gleichen Gebühr gibt, werden diejenigen mit der niedrigsten TTL bevorzugt.

\ In Beispiel 2.7 veranschaulichen wir, wie die Leistung von Greedy von der Diskontrate abhängen kann.

\ Beispiel 2.7. Wir untersuchen die Leistung von Greedy angesichts des folgenden Gegners ψ.

\

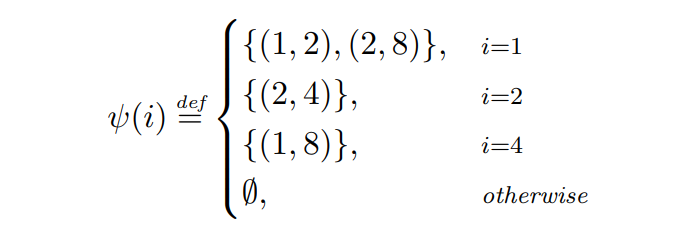
\ Der von ψ definierte Transaktionsplan ist in Abb. 1 dargestellt. In Runde 1 sendet der Gegner zwei Transaktionen: (1, 2), die am Ende der Runde abläuft und eine Gebühr von 2 hat, und (2, 4), die eine Gebühr von 4 zahlt und am Ende der nächsten Runde abläuft. Da Greedy Transaktionen mit höheren Gebühren priorisiert, wird es (2, 4) zuweisen, während die andere Transaktion abläuft. In der nächsten Runde sendet der Gegner eine einzelne Transaktion mit einer TTL von 2 und einer Gebühr von 6, die die einzige ist, die Greedy in dieser Runde zur Verfügung steht, und daher zugewiesen wird. In Schritt 3 sendet der Gegner keine Transaktionen, und in Schritt 4 wird eine Transaktion (1, 8) gesendet und dann von Greedy zugewiesen.

\

\

\ In Lemma 2.8 begrenzen wir das Wettbewerbsverhältnis von Greedy als Funktion der Diskontrate.

\

\

\

\

:::info Autoren:

(1) Yotam Gafni, Weizmann Institute ([e-mail]);

(2) Aviv Yaish, The Hebrew University, Jerusalem ([e-mail]).

:::

---

:::info Dieses Paper ist auf arxiv verfügbar unter der CC BY 4.0 DEED Lizenz.

:::

\