Eine einfachere Formel für Kurvenapproximation mit Bogensegmenten

Inhaltsverzeichnis

ZUSAMMENFASSUNG

1 EINLEITUNG

2 ABFLACHUNG UND BOGENNÄHERUNG VON KURVEN

3 EULER-SPIRALEN UND IHRE PARALLELKURVEN

4 ABGEFLACHTE PARALLELKURVEN

5 FEHLERMETRIKEN FÜR DIE APPROXIMATION DURCH BÖGEN

6 EVOLUTEN

7 UMWANDLUNG VON KUBISCHEN BÉZIERS ZU EULER-SPIRALEN

8 GPU-IMPLEMENTIERUNG

9 ERGEBNISSE

SCHLUSSFOLGERUNGEN, ZUKÜNFTIGE ARBEIT UND REFERENZEN

\

FEHLERMETRIKEN FÜR DIE APPROXIMATION DURCH BÖGEN

Das Problem der Approximation einer Kurve durch eine Folge von Bogensegmenten ist in der Literatur ausführlich behandelt, aber keine der veröffentlichten Lösungen ist für unsere Anwendung geeignet. Das spezifische Problem der Approximation einer Euler-Spirale durch Bögen wird in Meek und Walton [2004] mit einem adaptiven "Schneiden und Messen"-Unterteilungsschema betrachtet, aber ihre Lösung ist von schlechter Qualität; sie skaliert mit 𝑂(1/𝑛 2 ), während 𝑂(1/𝑛 3 ) erreichbar ist. Das Ergebnis wurde von Narayan [2014] "geringfügig" verbessert.

\ Die Literatur enthält auch optimale Ergebnisse, nämlich Maier [2014] und Nuntawisuttiwong und Dejdumrong [2021], aber zu erheblichen Kosten; beide Ansätze beanspruchen eine Zeitkomplexität von 𝑂(𝑛 2 ). Die Gemeinsamkeit all dieser Ergebnisse ist, dass sie ein schwierigeres Problem lösen: Sie übernehmen die Einschränkung, dass die erzeugte Bogensequenz 𝐺 1 kontinuierlich ist. Obwohl für viele Anwendungen wünschenswert, ist diese Einschränkung für das Rendern eines Strichkonturs nicht erforderlich.

\ Selbst mit dieser gelockerten Einschränkung sind die Winkelunstetigkeiten einer Bogenapproximation im Vergleich zur Abflachung zu Linien winzig. Unser Ansatz basiert auf einer einfachen Fehlermetrik, die der für die Abflachung zu Liniensegmenten ähnelt. Die Details der Metrik (insbesondere die Abstimmung der Konstanten) wurden empirisch ermittelt, obwohl wir vermuten, dass strengere analytische Grenzen erzielt werden könnten. In der Praxis funktioniert es tatsächlich sehr gut; der beste Weg, dies zu beobachten, ist ein interaktives Testwerkzeug, das in den ergänzenden Materialien bereitgestellt wird.

Die vorgeschlagene Fehlermetrik ist wie folgt. Der geschätzte Abstandsfehler für eine Kurve der Länge 𝑠ˆ ist:

𝑑 ≈ 1 120 ∫ 𝑠ˆ 0 3 √︁ |𝜅 ′ (𝑠)|𝑑𝑠!3

Für ein Euler-Spiralsegment ist 𝜅 ′ (𝑠) konstant und somit wird diese Fehlermetrik nahezu trivial. Mit 𝑛 Unterteilungen ist der geschätzte Abstand einfach 𝑠 3𝜅 ′ 120𝑛 3 . Durch Auflösen nach 𝑛 erhalten wir 𝑛 = 𝑠 3 √︃ |𝜅 ′ | 120𝑑 Unterteilungen, und diese werden gleichmäßig nach Bogenlänge aufgeteilt, da die Unterteilungsdichte über die Kurve konstant ist, genau wie bei der Abflachung von Bögen zu Linien. Bemerkenswerterweise ist die Approximation einer Euler-Spiralparallelkurve durch Bogensegmente fast so einfach wie die für Euler-Spiralen zu Bögen.

\ Wie bei der Abflachung zu Linien ist der Parameter für die Kurve die Bogenlänge der ursprünglichen Euler-Spirale. Die Unterteilungsdichte ist dann konstant, und es ist nur eine kleine Anpassung der Formel zur Berechnung der Anzahl der Unterteilungen erforderlich, wobei die zusätzliche Krümmungsvariation durch den Versatz um ℎ (die halbe Linienbreite) berücksichtigt wird. Die überarbeitete Formel lautet:

𝑛 = 𝑠 3 √︂ |𝜅 ′ | (1 + 0.4|ℎ𝑠𝜅′ |) 120𝑑

Diese Formel wurde empirisch durch Kurvenanpassung gemessener Fehlerwerte aus der Approximation von Euler-Spiralparallelkurven zu Bögen bestimmt, wurde aber auch durch die Anwendung der allgemeinen Fehlermetrikformel auf die analytischen Gleichungen für Euler-Spiralparallelkurven und das Weglassen höherer Terme inspiriert. Eine strengere Ableitung, idealerweise mit festen Fehlergrenzen, bleibt als zukünftige Arbeit bestehen.

\ Eine Konsequenz dieser Formel ist, dass, da der Fehler in Bezug auf den Absolutwert von ℎ unabhängig vom Vorzeichen ist, dieselbe Bogenapproximation für beide Seiten eines Strichs verwendet werden kann. Siehe Abbildung 8 für einen Vergleich zwischen der Abflachung zu einer Polylinie und der Approximation mit Bogensegmenten. Die Bogensegmentversion hat bei gleicher Toleranz viel weniger Segmente, während sie eine sehr hohe visuelle Qualität bewahrt.

EVOLUTEN

In der prinzipiellen, korrekten Spezifikation für das Streichen [19] sind Parallelkurven nur für Segmente ausreichend, in denen die Krümmung

\

\ die reziproke Halbbreite nicht überschreitet. Wenn sie dies tut, müssen zusätzliche Segmente gezeichnet werden, einschließlich Evoluten der ursprünglichen Kurve. Im Allgemeinen ist die Evolute einer kubischen Bézier-Kurve eine sehr komplexe Kurve, die Approximationstechniken erfordert. Im Gegensatz dazu ist die Evolute einer Euler-Spirale (𝜅 = 𝑎𝑠) eine andere Spirale mit einer einfachen Cesàro-Gleichung, nämlich 𝜅 = −𝑎 −1 𝑠 −3 , ein Beispiel für das allgemeine Ergebnis, dass die Evolute einer log-ästhetischen Kurve eine andere log-ästhetische Kurve ist [26].

\ Die Abflachung dieser Evolute ist ebenfalls unkompliziert; die Unterteilungsdichte ist proportional zu 𝑠 −0.5 , wobei 𝑠 der Bogenlängenparameter der zugrunde liegenden Euler-Spirale ist (und so übersetzt, dass 𝑠 = 0 der Wendepunkt ist). Somit ist das Integral 2 √ 𝑠, und das inverse Integral ist einfach das Quadrieren. Daher ist die Abflachung der Evolute einer Euler-Spirale einfacher als die Abflachung ihrer Parallelkurve. D

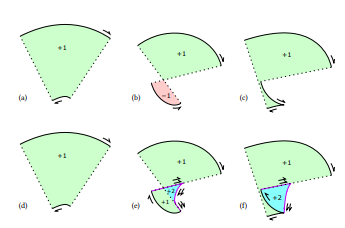
\ ie Wirkung des Hinzufügens von Evoluten, um eine starke Korrektheit zu erreichen, wird in Abbildung 9 gezeigt. Die zusätzlichen Evolutensegmente und Verbindungslinien werden zweimal ausgegeben, um die Windungszahlen konsistent zu machen und einen wasserdichten Umriss zu erzeugen. Alle Windungszahlen sind positiv, sodass das Rendern mit der Nicht-Null-Windungsregel ein korrektes endgültiges Rendering ergibt.

:::info Autoren:

1. Raph Levien
2. Arman Uguray

:::

:::info Dieses Paper ist auf arxiv verfügbar unter CC 4.0 Lizenz.

:::

\