Cách Thuật Toán Tham Lam Định Hình Phần Thưởng Của Thợ Đào Trong Các Mạng Blockchain
Bảng liên kết
Tóm tắt và 1. Giới thiệu
1.1 Cách tiếp cận của chúng tôi
1.2 Kết quả & Lộ trình của chúng tôi
1.3 Các nghiên cứu liên quan
-
Mô hình và Khởi động và 2.1 Mô hình Blockchain
2.2 Thợ đào
2.3 Mô hình trò chơi
2.4 Khởi động: Hàm phân bổ tham lam
-
Trường hợp xác định và 3.1 Giới hạn trên xác định
3.2 Lớp hàm phân bổ thiên vị tức thời
-
Trường hợp ngẫu nhiên
-
Thảo luận và Tài liệu tham khảo
- A. Các chứng minh còn thiếu cho Phần 2, 3
- B. Các chứng minh còn thiếu cho Phần 4
- C. Bảng thuật ngữ
\
2.3 Mô hình trò chơi
Chúng tôi xem xét một trò chơi giữa đối thủ và thợ đào. Quan điểm này nhằm lượng hóa mức độ doanh thu mà thợ đào có thể mất do kiến thức không đầy đủ về các giao dịch trong tương lai khi phân bổ các giao dịch hiện đã biết vào khối sắp tới. Về mặt này, người dùng đang hoạt động trong hệ thống có thể được coi là một "tự nhiên" toàn tri đối nghịch, tạo ra một lịch trình giao dịch trong trường hợp xấu nhất. Một hàm phân bổ không có kiến thức về các giao dịch trong tương lai sẽ được gửi bởi đối thủ, và vì vậy việc lập kế hoạch tối ưu dựa trên thông tin một phần được tiết lộ bởi các giao dịch trước đó có thể không phải là hướng hành động tốt nhất. Tuy nhiên, khá đáng ngạc nhiên, sau này chúng tôi chỉ ra rằng thực tế là như vậy. Với tỷ lệ chiết khấu của thợ đào, có một căng thẳng về mặt khái niệm giữa việc bao gồm các giao dịch có phí lớn nhất và những giao dịch có TTL thấp nhất. Do đó, chất lượng của hàm phân bổ x được lượng hóa bằng cách so sánh nó với hàm tốt nhất có thể x′, khi đối mặt với trường hợp xấu nhất của đối thủ ψ. Số lượng kết quả được gọi là tỷ lệ cạnh tranh của x. Để duy trì tương thích với tài liệu về lập lịch gói, chúng tôi định nghĩa tỷ lệ cạnh tranh là hiệu suất ngoại tuyến tốt nhất có thể chia cho hiệu suất trực tuyến của hàm phân bổ, thay vì ngược lại, và vì vậy chúng tôi có Rx ≥ 1. Giới hạn trên sau đó đạt được bằng cách tìm một hàm phân bổ đảm bảo hiệu suất tốt, và giới hạn dưới đạt được bằng cách chứng minh rằng không có hàm phân bổ nào có thể đảm bảo hiệu suất tốt hơn.
\ \ 
\ \ \
2.4 Khởi động: Hàm phân bổ tham lam
Hàm phân bổ Tham lam, được định nghĩa trong Định nghĩa 2.6, có lẽ là một thuật toán cổ điển cho vấn đề lập lịch gói, và đã được khám phá bởi các tài liệu trước đây cho trường hợp không chiết khấu. Hơn nữa, bằng chứng thực nghiệm cho thấy hầu hết các thợ đào phân bổ giao dịch vào các khối một cách tham lam. Các công trình trước đây cho thấy trong Bitcoin và Ethereum, các giao dịch trả phí cao hơn thường có thời gian chờ mempool thấp hơn, nghĩa là chúng được đưa vào các khối tương đối nhanh chóng [MACG20; PORH22; TFWM21; LLNZZZ22]. Thật vậy, các thuật toán lựa chọn giao dịch mặc định cho Bitcoin Core (triển khai tham chiếu cho các máy khách Bitcoin) và geth (máy khách thực thi phổ biến nhất của Ethereum), ưu tiên các giao dịch dựa trên phí của chúng, mặc dù hành vi mặc định của cả hai có thể bị ghi đè. Do đó, việc xem xét hiệu suất của phương pháp này là điều đáng quan tâm.
\ Định nghĩa 2.6 (Hàm phân bổ Tham lam). Cho một tập hợp giao dịch S, hàm phân bổ Tham lam chọn giao dịch trả phí cao nhất có trong tập S, bỏ qua TTL:
\ 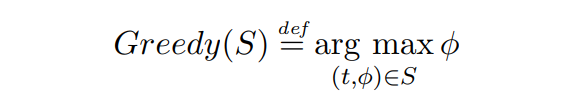
\ Trong trường hợp có nhiều giao dịch có cùng phí, những giao dịch có TTL thấp nhất được ưu tiên.
\ Trong Ví dụ 2.7, chúng tôi minh họa cách hiệu suất của Tham lam có thể phụ thuộc vào tỷ lệ chiết khấu.
\ Ví dụ 2.7. Chúng tôi xem xét hiệu suất của Tham lam với đối thủ ψ sau đây.
\ 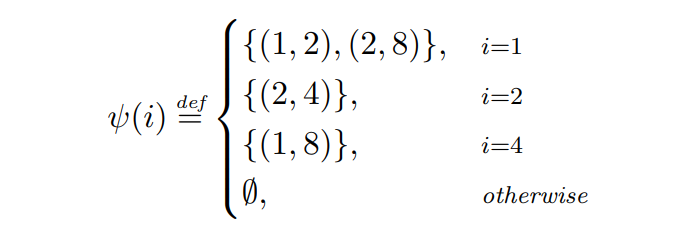
\ Lịch trình giao dịch được định nghĩa bởi ψ được mô tả trong Hình 1. Ở lượt 1, đối thủ phát sóng hai giao dịch: (1, 2) hết hạn vào cuối lượt và có phí là 2, và (2, 4) trả phí bằng 4 và hết hạn vào cuối lượt tiếp theo. Bởi vì Tham lam ưu tiên các giao dịch có phí cao hơn, nó sẽ phân bổ (2, 4), trong khi để giao dịch kia hết hạn. Trong lượt tiếp theo, đối thủ phát sóng một giao dịch duy nhất với TTL là 2 và phí là 6, đây là giao dịch duy nhất có sẵn cho Tham lam ở lượt đó, và do đó sẽ được phân bổ. Ở bước 3, đối thủ không phát ra bất kỳ giao dịch nào, và ở bước 4, một giao dịch (1, 8) được phát sóng và sau đó được phân bổ bởi Tham lam.
\ 
\ 
\ Trong Bổ đề 2.8, chúng tôi giới hạn tỷ lệ cạnh tranh của Tham lam, như một hàm của tỷ lệ chiết khấu.
\ 
\ 
\ 
\
:::info Tác giả:
(1) Yotam Gafni, Weizmann Institute (yotam.gafni@gmail.com);
(2) Aviv Yaish, The Hebrew University, Jerusalem (aviv.yaish@mail.huji.ac.il).
:::
:::info Bài báo này có sẵn trên arxiv theo giấy phép CC BY 4.0 DEED.
:::
\
Có thể bạn cũng thích

Bản Tin Sáng Châu Á: BTC Ổn Định Quanh Mức 90k Khi Thanh Khoản Cạn Kiệt và Việc Cắt Giảm Lãi Suất của Fed Đã Được Định Giá Hoàn Toàn
Sao chép liên kếtX (Twitter)LinkedInFacebookEmail

Tại sao các ngân hàng có nguy cơ bị hạ bậc tín dụng theo Fitch
