Як жадібний алгоритм формує винагороди майнерів у блокчейн-мережах

Таблиця посилань

Анотація та 1. Вступ

1.1 Наш підхід

1.2 Наші результати та дорожня карта

1.3 Пов'язані роботи

1. Модель та розминка та 2.1 Модель блокчейну

   2.2 Майнер

   2.3 Ігрова модель

   2.4 Розминка: функція жадібного розподілу

2. Детерміністичний випадок та 3.1 Детерміністична верхня межа

   3.2 Клас функцій розподілу з упередженням до негайності

3. Випадковий випадок

4. Обговорення та посилання

• A. Відсутні докази для розділів 2, 3
• B. Відсутні докази для розділу 4
• C. Глосарій

\

2.3 Ігрова модель

Ми розглядаємо гру між супротивником та майнером. Ця перспектива спрямована на кількісну оцінку того, скільки доходу майнер може втратити через неповне знання майбутніх транзакцій при розподілі відомих на даний момент транзакцій до наступного блоку. У цьому відношенні активних користувачів системи можна розглядати як всезнаючу "природу", що створює найгірший сценарій розкладу транзакцій. Функція розподілу не має знань про майбутні транзакції, які будуть надіслані супротивником, тому оптимальне планування на основі часткової інформації, яка розкривається попередніми транзакціями, може не бути найкращим курсом дій. Однак, дещо дивно, ми пізніше показуємо, що це насправді так. Враховуючи ставку дисконтування майнера, існує концептуальна напруга між включенням транзакцій з найбільшою комісією та тими, що мають найнижчий TTL. Таким чином, якість функції розподілу x кількісно визначається шляхом порівняння її з найкращою можливою функцією x′, коли стикається з найгіршим випадком супротивника ψ. Отримана величина називається конкурентним співвідношенням x. Щоб залишатися сумісним з літературою про планування пакетів, ми визначаємо конкурентне співвідношення як найкращу можливу офлайн-продуктивність, поділену на онлайн-продуктивність функції розподілу, а не навпаки, і тому ми маємо Rx ≥ 1. Верхня межа досягається шляхом знаходження функції розподілу, яка гарантує хорошу продуктивність, а нижня межа досягається шляхом доведення того, що жодна функція розподілу не може гарантувати кращу продуктивність.

\ \

\ \ \

2.4 Розминка: функція жадібного розподілу

Функція розподілу Greedy, визначена у визначенні 2.6, можливо, є класичним алгоритмом для проблеми планування пакетів, і була досліджена попередньою літературою для недисконтованого випадку. Крім того, емпіричні дані свідчать про те, що більшість майнерів жадібно розподіляють транзакції по блоках. Попередні роботи показують, що в Bitcoin та Ethereum транзакції, які сплачують вищі комісії, зазвичай мають менший час очікування в мемпулі, що означає, що вони відносно швидко включаються в блоки [MACG20; PORH22; TFWM21; LLNZZZ22]. Дійсно, алгоритми вибору транзакцій за замовчуванням для Bitcoin Core (еталонна реалізація для клієнтів Bitcoin) та geth (найпопулярніший клієнт виконання Ethereum) пріоритезують транзакції на основі їхніх комісій, хоча поведінка за замовчуванням обох може бути перевизначена. Таким чином, цікаво побачити продуктивність цього підходу.

\ Визначення 2.6 (Функція жадібного розподілу). Враховуючи деякий набір транзакцій S, функція жадібного розподілу вибирає транзакцію з найвищою оплатою, присутню в наборі S, ігноруючи TTL:

\

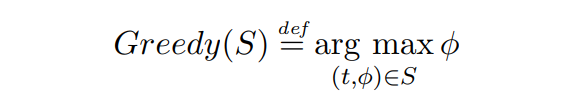
\ У випадку, якщо є кілька транзакцій з однаковою комісією, перевага надається тим, які мають найнижчий TTL.

\ У прикладі 2.7 ми ілюструємо, як продуктивність Greedy може залежати від ставки дисконтування.

\ Приклад 2.7. Ми розглядаємо продуктивність Greedy з огляду на наступного супротивника ψ.

\

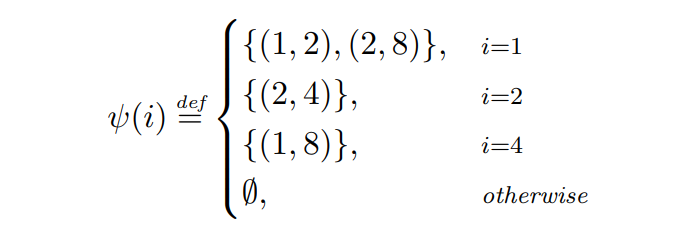
\ Розклад транзакцій, визначений ψ, зображено на рис. 1. На ході 1 супротивник транслює дві транзакції: (1, 2), яка закінчується в кінці ходу і має комісію 2, і (2, 4), яка сплачує комісію, рівну 4, і закінчується в кінці наступного ходу. Оскільки Greedy пріоритезує транзакції з вищими комісіями, він розподілить (2, 4), дозволяючи іншій транзакції закінчитися. На наступному ході супротивник транслює одну транзакцію з TTL 2 і комісією 6, яка є єдиною доступною для Greedy на цьому ході, і тому буде розподілена. На кроці 3 супротивник не випускає жодних транзакцій, а на кроці 4 транзакція (1, 8) транслюється, а потім розподіляється Greedy.

\

\

\ У лемі 2.8 ми обмежуємо конкурентне співвідношення Greedy як функцію ставки дисконтування.

\

\

\

\

:::info Автори:

(1) Йотам Гафні, Інститут Вейцмана ([e-mail]);

(2) Авів Яіш, Єврейський університет, Єрусалим ([e-mail]).

:::

---

:::info Ця стаття доступна на arxiv за ліцензією CC BY 4.0 DEED.

:::

\