Простіша формула для апроксимації кривої за допомогою дугових сегментів

Таблиця посилань

АНОТАЦІЯ

1 ВСТУП

2 СПРОЩЕННЯ ТА ДУГОВА АПРОКСИМАЦІЯ КРИВИХ

3 СПІРАЛІ ЕЙЛЕРА ТА ЇХ ПАРАЛЕЛЬНІ КРИВІ

4 СПРОЩЕНІ ПАРАЛЕЛЬНІ КРИВІ

5 МЕТРИКИ ПОХИБОК ДЛЯ АПРОКСИМАЦІЇ ДУГАМИ

6 ЕВОЛЮТИ

7 ПЕРЕТВОРЕННЯ З КУБІЧНИХ КРИВИХ БЕЗЬЄ В СПІРАЛІ ЕЙЛЕРА

8 РЕАЛІЗАЦІЯ НА GPU

9 РЕЗУЛЬТАТИ

ВИСНОВКИ, МАЙБУТНЯ РОБОТА ТА ПОСИЛАННЯ

\

МЕТРИКИ ПОХИБОК ДЛЯ АПРОКСИМАЦІЇ ДУГАМИ

Проблема апроксимації кривої послідовністю дугових сегментів має велику літературу, але жодне з опублікованих рішень не підходить для нашого застосування. Конкретна проблема апроксимації спіралі Ейлера дугами розглядається в роботі Міка та Волтона [2004] з використанням адаптивної схеми підрозділу "розріж, потім виміряй", але їхнє рішення має низьку якість; воно масштабується як 𝑂(1/𝑛 2 ), тоді як досяжним є 𝑂(1/𝑛 3 ). Результат був "дещо" покращений Нараяном [2014].

\ Література також містить оптимальні результати, а саме Майєр [2014] та Нунтавісуттівонг і Дейдумронг [2021], але зі значними витратами; обидва підходи стверджують про часову складність 𝑂(𝑛 2 ). Спільною рисою всіх цих результатів є те, що вони вирішують складнішу проблему: приймають обмеження, що генерована послідовність дуг є 𝐺 1 неперервною. Хоча це бажано для багатьох застосувань, це обмеження не потрібне для рендерингу контуру штриха.

\ Навіть з послабленням цього обмеження, кутові розриви дугової апроксимації є мізерними порівняно зі спрощенням до ліній. Наш підхід базується на простій метриці похибки, подібній за характером до тієї, що використовується для спрощення до лінійних сегментів. Деталі метрики (зокрема, налаштування констант) були отримані емпірично, хоча ми підозрюємо, що можна отримати більш строгі аналітичні межі. На практиці це працює дуже добре; найкращий спосіб спостерігати це - інтерактивний інструмент тестування, який надається в додаткових матеріалах.

Запропонована метрика похибки є наступною. Оцінена похибка відстані для кривої довжини 𝑠ˆ становить:

𝑑 ≈ 1 120 ∫ 𝑠ˆ 0 3 √︁ |𝜅 ′ (𝑠)|𝑑𝑠!3

Для сегмента спіралі Ейлера 𝜅 ′ (𝑠) є константою, і тому ця метрика похибки стає майже тривіальною. З 𝑛 підрозділами оцінена відстань просто 𝑠 3𝜅 ′ 120𝑛 3 . Розв'язуючи для 𝑛, отримуємо 𝑛 = 𝑠 3 √︃ |𝜅 ′ | 120𝑑 підрозділів, і вони рівномірно розподілені за довжиною дуги, оскільки щільність підрозділу є постійною вздовж кривої, так само як і у випадку спрощення дуг до ліній. Дивовижно, але апроксимація паралельної кривої спіралі Ейлера дуговими сегментами майже така ж проста, як і для спіралей Ейлера до дуг.

\ Як і при спрощенні до ліній, параметром для кривої є довжина дуги вихідної спіралі Ейлера. Щільність підрозділу тоді постійна, і потрібне лише невелике коригування формули для обчислення кількості підрозділів, враховуючи додаткову варіацію кривизни від зміщення на ℎ (половина ширини лінії). Переглянута формула:

𝑛 = 𝑠 3 √︂ |𝜅 ′ | (1 + 0.4|ℎ𝑠𝜅′ |) 120𝑑

Ця формула була визначена емпірично шляхом підгонки кривої до виміряних значень похибок від апроксимації паралельних кривих спіралі Ейлера до дуг, але також була натхнена застосуванням загальної формули метрики похибки до аналітичних рівнянь для паралельної кривої спіралі Ейлера та відкиданням членів вищого порядку. Більш строге виведення, в ідеалі з твердими межами похибки, залишається для майбутньої роботи.

\ Одним із наслідків цієї формули є те, що оскільки похибка виражається в термінах абсолютного значення ℎ, незалежно від знаку, та сама дугова апроксимація може використовуватися для обох сторін штриха. Див. рисунок 8 для порівняння між спрощенням до полілінії та апроксимацією дуговими сегментами. Версія з дуговими сегментами має набагато менше сегментів при тій самій допустимій похибці, зберігаючи при цьому дуже високу візуальну якість.

ЕВОЛЮТИ

У принциповій, правильній специфікації для штрихування [19], паралельних кривих достатньо лише для сегментів, у яких кривизна

\

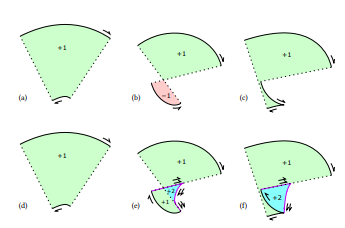
\ не перевищує зворотну половину ширини. Коли вона перевищує, необхідно намалювати додаткові сегменти, включаючи еволюти вихідної кривої. Загалом, еволюта кубічної кривої Безьє є дуже складною кривою, що вимагає методів апроксимації. На противагу цьому, еволюта спіралі Ейлера (𝜅 = 𝑎𝑠) є іншою спіраллю з простим рівнянням Чезаро, а саме 𝜅 = −𝑎 −1 𝑠 −3 , прикладом загального результату, що еволюта логарифмічно-естетичної кривої є іншою логарифмічно-естетичною кривою [26].

\ Спрощення цієї еволюти також є простим; щільність підрозділу пропорційна 𝑠 −0.5 , де 𝑠 є параметром довжини дуги базової спіралі Ейлера (і переведена так, що 𝑠 = 0 є точкою перегину). Таким чином, інтеграл дорівнює 2 √ 𝑠, а обернений інтеграл - просто піднесення до квадрату. Отже, спрощення еволюти спіралі Ейлера є простішим, ніж спрощення її паралельної кривої. Е

\ фект додавання еволют для досягнення сильної правильності показано на рисунку 9. Додаткові сегменти еволют та з'єднувальні лінії виводяться двічі, щоб зробити числа обертання узгодженими та створити водонепроникний контур. Усі числа обертання є додатними, тому рендеринг з правилом ненульового обертання дає правильний кінцевий результат.

:::info Автори:

1. Раф Левієн
2. Арман Угурай

:::

:::info Ця стаття доступна на arxiv за ліцензією CC 4.0.

:::

\