Understanding Approximation Error and Query Complexity in WormHole Routing

Table of Links

Abstract and 1. Introduction

1.1 Our Contribution

1.2 Setting

1.3 The algorithm

1. Related Work

2. Algorithm

   3.1 The Structural Decomposition Phase

   3.2 The Routing Phase

   3.3 Variants of WormHole

3. Theoretical Analysis

   4.1 Preliminaries

   4.2 Sublinearity of Inner Ring

   4.3 Approximation Error

   4.4 Query Complexity

4. Experimental Results

   5.1 WormHole𝐸, WormHole𝐻 and BiBFS

   5.2 Comparison with index-based methods

   5.3 WormHole as a primitive: WormHole𝑀

References

4.3 Approximation Error

Now that we have a sublinear inner ring that contains the Chung-Lu core, we must show that routing paths through it incurs only a small penalty. Intuitively, the larger the inner ring, the easier this is to satisfy: if the inner ring is the whole graph, the statement holds trivially. Therefore the challenge lies in showing that we can achieve a strong guarantee in terms of accuracy even with a sublinear inner ring. We prove that WormHole incurs an additive error at most 𝑂(loglog𝑛) for all pairs, which is much smaller than the diameter Θ(log𝑛).

\

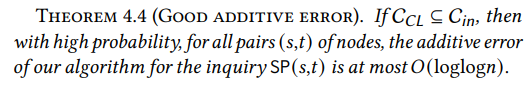
\ The above result holds with high probability even in the worst case. Namely, for all pairs (𝑠,𝑡) of vertices in the graph, the length of the path returned by WormHole is at most𝑂(loglog𝑛) higher than the actual distance between 𝑠 and 𝑡. This trivially implies that the average additive error of WormHole is, with high probability, bounded by the same amount.

\

\

4.4 Query Complexity

Recall the node query model in this paper (see §1.2): starting from a single node, we are allowed to iteratively make queries, where each query retrieves the neighbor list of a node 𝑣 of our choice. We are interested in the query complexity, i.e., the number of queries required to conduct certain operations.

\ \

\ \ The first result is the upper bound on our performance.

\ \

\ \ Proof Sketch. For a given inquiry SP(𝑢, 𝑣), we give an upper bound on the query complexity of the BFS that starts at 𝑢, and similarly for𝑣; the total query complexity is the sum of these two quantities.

\ \

\ \ \

\ \ \

\ \ \

\ \ \

\ \

:::info Authors:

(1) Talya Eden, Bar-Ilan University ([e-mail]);

(2) Omri Ben-Eliezer, MIT ([e-mail]);

(3) C. Seshadhri, UC Santa Cruz ([e-mail]).

:::

---

:::info This paper is available on arxiv under CC BY 4.0 license.

:::

\