Uma Fórmula Mais Simples para Aproximação de Curvas Usando Segmentos de Arco

Tabela De Links

RESUMO

1 INTRODUÇÃO

2 ACHATAMENTO E APROXIMAÇÃO DE ARCO DE CURVAS

3 ESPIRAIS DE EULER E SUAS CURVAS PARALELAS

4 CURVAS PARALELAS ACHATADAS

5 MÉTRICAS DE ERRO PARA APROXIMAÇÃO POR ARCOS

6 EVOLUTAS

7 CONVERSÃO DE BÉZIERS CÚBICAS PARA ESPIRAIS DE EULER

8 IMPLEMENTAÇÃO GPU

9 RESULTADOS

CONCLUSÕES, TRABALHO FUTURO E REFERÊNCIAS

\

MÉTRICAS DE ERRO PARA APROXIMAÇÃO POR ARCOS

O problema de aproximar uma curva por uma sequência de segmentos de arco tem extensa literatura, mas nenhuma das soluções publicadas é adequada para a nossa aplicação. O problema específico de aproximar uma espiral de Euler por arcos é considerado em Meek e Walton [2004] usando um esquema de subdivisão adaptativa "cortar e depois medir", mas a solução deles tem baixa qualidade; escala como 𝑂(1/𝑛 2 ), enquanto 𝑂(1/𝑛 3 ) é alcançável. O resultado foi melhorado "ligeiramente" por Narayan [2014].

\ A literatura também contém resultados ótimos, nomeadamente Maier [2014] e Nuntawisuttiwong e Dejdumrong [2021], mas a um custo considerável; ambas as abordagens afirmam complexidade de tempo 𝑂(𝑛 2 ). A linha comum para todos estes resultados é que estão a resolver um problema mais difícil: adotar a restrição de que a sequência de arcos gerada é contínua 𝐺 1. Embora desejável para muitas aplicações, esta restrição não é necessária para renderizar um contorno de traço.

\ Mesmo com esta restrição relaxada, as descontinuidades de ângulo de uma aproximação de arco são minúsculas em comparação com o achatamento para linhas. A nossa abordagem baseia-se numa métrica de erro simples, semelhante em sabor à utilizada para achatamento para segmentos de linha. Os detalhes da métrica (em particular, o ajuste de constantes) foram obtidos empiricamente, embora suspeitemos que limites analíticos mais rigorosos possam ser obtidos. Na prática, funciona muito bem; a melhor maneira de observar isso é uma ferramenta de teste interativa, que é fornecida nos materiais suplementares.

A métrica de erro proposta é a seguinte. O erro de distância estimado para uma curva de comprimento 𝑠ˆ é:

𝑑 ≈ 1 120 ∫ 𝑠ˆ 0 3 √︁ |𝜅 ′ (𝑠)|𝑑𝑠!3

Para um segmento de espiral de Euler, 𝜅 ′ (𝑠) é constante e, portanto, esta métrica de erro torna-se quase trivial. Com 𝑛 subdivisões, a distância estimada é simplesmente 𝑠 3𝜅 ′ 120𝑛 3 . Resolvendo para 𝑛, obtemos 𝑛 = 𝑠 3 √︃ |𝜅 ′ | 120𝑑 subdivisões, e estas são divididas uniformemente pelo comprimento do arco, já que a densidade de subdivisão é constante ao longo da curva, tal como no caso de achatamento de arcos para linhas. Notavelmente, a aproximação de uma curva paralela de espiral de Euler por segmentos de arco é quase tão simples quanto a de espirais de Euler para arcos.

\ Como no achatamento para linhas, o parâmetro para a curva é o comprimento do arco da espiral de Euler originária. A densidade de subdivisão é então constante, e apenas um pequeno ajuste é necessário na fórmula para calcular o número de subdivisões, tendo em conta a variação adicional de curvatura do deslocamento por ℎ (a meia largura da linha). A fórmula revista é:

𝑛 = 𝑠 3 √︂ |𝜅 ′ | (1 + 0.4|ℎ𝑠𝜅′ |) 120𝑑

Esta fórmula foi determinada empiricamente por ajuste de curva de valores de erro medidos da aproximação de curvas paralelas de espiral de Euler para arcos, mas também foi inspirada pela aplicação da fórmula geral de métrica de erro às equações analíticas para curva paralela de espiral de Euler, e eliminando termos de ordem superior. Uma derivação mais rigorosa, idealmente com limites de erro firmes, permanece como trabalho futuro.

\ Uma consequência desta fórmula é que, uma vez que o erro está em termos do valor absoluto de ℎ, independente do sinal, a mesma aproximação de arco pode ser usada para ambos os lados de um traço. Veja a Figura 8 para uma comparação entre achatamento para uma polilinha e aproximação com segmentos de arco. A versão de segmento de arco tem muito menos segmentos com a mesma tolerância, enquanto preserva uma qualidade visual muito alta.

EVOLUTAS

Na especificação correta e fundamentada para traçado [19], as curvas paralelas são suficientes apenas para segmentos nos quais a curvatura

\

\ não excede a meia largura recíproca. Quando excede, segmentos adicionais devem ser desenhados, incluindo evolutas da curva original. Em geral, a evoluta de uma Bézier cúbica é uma curva muito complexa, exigindo técnicas de aproximação. Em contraste, a evoluta de uma espiral de Euler (𝜅 = 𝑎𝑠) é outra espiral com uma equação de Cesàro simples, nomeadamente 𝜅 = −𝑎 −1 𝑠 −3 , uma instância do resultado geral de que a evoluta de uma curva log-estética é outra curva log-estética [26].

\ O achatamento desta evoluta também é simples; a densidade de subdivisão é proporcional a 𝑠 −0.5 onde 𝑠 é o parâmetro de comprimento de arco da espiral de Euler subjacente (e traduzido para que 𝑠 = 0 seja o ponto de inflexão). Assim, o integral é 2 √ 𝑠, e o integral inverso é apenas elevar ao quadrado. Portanto, o achatamento da evoluta de uma espiral de Euler é mais simples do que o achatamento da sua curva paralela. O

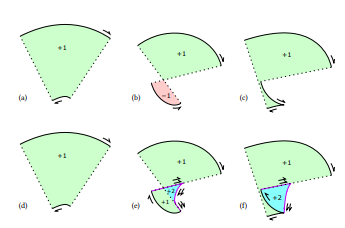
\ efeito de adicionar evolutas para alcançar forte correção é mostrado na Figura 9. Os segmentos adicionais de evoluta e linhas de conexão são produzidos duas vezes, para tornar os números de enrolamento consistentes e produzir um contorno estanque. Todos os números de enrolamento são positivos, então a renderização com a regra de enrolamento não-zero produz uma renderização final correta.

:::info Autores:

1. Raph Levien
2. Arman Uguray

:::

:::info Este artigo está disponível no arxiv sob licença CC 4.0.

:::

\