アークセグメントを使用した曲線近似のためのよりシンプルな公式

リンク一覧

要旨

1 はじめに

2 曲線の平坦化と円弧近似

3 オイラー螺旋とその平行曲線

4 平坦化された平行曲線

5 円弧による近似の誤差指標

6 エボリュート

7 3次ベジェ曲線からオイラー螺旋への変換

8 GPU実装

9 結果

結論、今後の課題および参考文献

\

円弧による近似の誤差指標

曲線を一連の円弧セグメントで近似する問題には膨大な文献がありますが、公開されている解決策はどれも私たちのアプリケーションには適していません。オイラー螺旋を円弧で近似するという特定の問題は、Meekと Walton [2004]によって「切断してから測定する」適応的分割スキームを使用して検討されていますが、彼らの解決策は品質が低く、𝑂(1/𝑛 2 )でスケールしますが、𝑂(1/𝑛 3 )は達成可能です。この結果はNarayan [2014]によって「わずかに」改善されました。

\ 文献には最適な結果も含まれています。具体的にはMaier [2014]とNuntawisuttiwongとDejdumrong [2021]ですが、かなりのコストがかかります。どちらのアプローチも𝑂(𝑛 2 )の時間複雑性を主張しています。これらすべての結果の共通点は、より難しい問題を解決していることです：生成された円弧シーケンスが𝐺 1 連続であるという制約を採用しています。多くのアプリケーションでは望ましいものの、この制約はストロークのアウトラインをレンダリングするには必要ありません。

\ この制約が緩和されても、円弧近似の角度の不連続性は線への平坦化と比較すると非常に小さいです。私たちのアプローチは、線分への平坦化のものと似た風味の単純な誤差指標に基づいています。指標の詳細（特に定数の調整）は経験的に得られましたが、より厳密な分析的境界が得られる可能性があると考えています。実際には非常にうまく機能します。それを観察する最良の方法は、補足資料で提供されているインタラクティブなテストツールです。

提案された誤差指標は次のとおりです。長さ𝑠ˆの曲線の推定距離誤差は：

𝑑 ≈ 1 120 ∫ 𝑠ˆ 0 3 √︁ |𝜅 ′ (𝑠)|𝑑𝑠!3

オイラー螺旋セグメントの場合、𝜅 ′ (𝑠)は定数であるため、この誤差指標はほぼ自明になります。𝑛分割では、推定距離は単に𝑠 3𝜅 ′ 120𝑛 3 です。𝑛について解くと、𝑛 = 𝑠 3 √︃ |𝜅 ′ | 120𝑑 分割が得られ、それらは曲線全体で分割密度が一定であるため、円弧長に沿って均等に分割されます。これは円弧を線に平坦化する場合と同様です。注目すべきことに、オイラー螺旋平行曲線の円弧セグメントによる近似は、オイラー螺旋を円弧に近似するのとほぼ同じくらい単純です。

\ 線への平坦化と同様に、曲線のパラメータは元のオイラー螺旋の円弧長です。分割密度はその後一定となり、分割数を計算する式にはわずかな調整だけが必要で、ℎ（半線幅）によるオフセットからの追加の曲率変化を考慮します。修正された式は：

𝑛 = 𝑠 3 √︂ |𝜅 ′ | (1 + 0.4|ℎ𝑠𝜅′ |) 120𝑑

この式は、オイラー螺旋平行曲線を円弧に近似する際の測定誤差値から曲線フィッティングによって経験的に決定されましたが、一般的な誤差指標式をオイラー螺旋平行曲線の解析式に適用し、高次の項を削除することからも着想を得ています。より厳密な導出、理想的には確固たる誤差境界を持つものは、今後の課題として残されています。

\ この式の一つの結果として、誤差が符号に関係なくℎの絶対値で表されるため、同じ円弧近似をストロークの両側に使用できます。ポリラインへの平坦化と円弧セグメントによる近似の比較については、図8をご覧ください。円弧セグメントバージョンは同じ許容範囲でセグメント数がはるかに少なく、非常に高い視覚的品質を維持しています。

エボリュート

原則に基づいた、正確なストローキングの仕様[19]では、平行曲線は曲率が

\

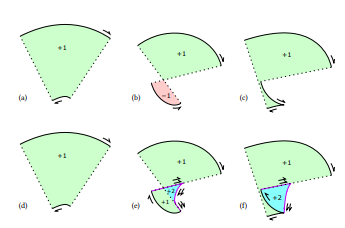
\ 半幅の逆数を超えないセグメントに対してのみ十分です。超える場合は、元の曲線のエボリュートを含む追加のセグメントを描画する必要があります。一般に、3次ベジェ曲線のエボリュートは非常に複雑な曲線であり、近似技術が必要です。対照的に、オイラー螺旋(𝜅 = 𝑎𝑠)のエボリュートは、単純なCesàro方程式を持つ別の螺旋です。具体的には𝜅 = −𝑎 −1 𝑠 −3 であり、これはログ美的曲線のエボリュートが別のログ美的曲線であるという一般的な結果の一例です[26]。

\ このエボリュートの平坦化も簡単です。分割密度は𝑠 −0.5 に比例します。ここで𝑠は基礎となるオイラー螺旋の円弧長パラメータです（そして𝑠 = 0が変曲点になるように変換されます）。したがって、積分は2 √ 𝑠であり、逆積分は単に二乗することです。したがって、オイラー螺旋のエボリュートの平坦化は、その平行曲線の平坦化よりも単純です。

\ 強い正確さを達成するためにエボリュートを追加する効果は図9に示されています。追加のエボリュートセグメントと接続線は、巻き数を一貫させ、水密のアウトラインを生成するために2回出力されます。すべての巻き数は正であるため、非ゼロ巻き数ルールでレンダリングすると、正確な最終レンダリングが得られます。

:::info 著者：

1. Raph Levien
2. Arman Uguray

:::

:::info この論文はCC 4.0ライセンスの下でarxivで入手可能です。

:::

\